Задача про сто монеток и десять орлов
Просмотров: 8215
19 июля 2017 года
Постановка задачи
"Месяц назад" (16 июня) в личку на сайте мне пришла замечательная задача от одного из посетителей. Обстоятельства, как это не редко бывает, сложились так, что времени на оформление решения долго не было. Итак:
У вас есть 100 монет, лежащих на столе. У каждой из них есть две стороны: «орел» и «решка». 10 монет «орлом» вверх и 90 «решкой» вверх. Вы не можете почувствовать, увидеть или как-то распознать, где какая сторона. Вам нужно поделить все монетки на две части так, чтобы в каждой из них было равное количество монеток, которые лежат «орлом» вверх
Примечание
Глава 0 не содержит решения поставленной задачи, но может быть полезна для общего кругозора.
Глава 0. Поворот не туда
Монетки лежат рандомно, оценить состояние ("орёл"-"решка") нельзя, известна только статистика "90 к 10". Моя болезненная тяга к теорверу, построила в голове вероятностную модель и увела решение не в то русло.
Сначала мне не понравилось неравномерное распределение. Ну, тут я додумался, что никто не запрещал подбрасывать монетки, инициализируя их состояние заново. Таким образом, мы можем перейти от распределения "9 к 1" к "1 к 1". Тем не менее, всегда остаётся вероятность разделить всю совокупность монет неудачно (и это ещё не принимая во внимание отсутствие гарантии получить равномерное распределение).
Потом были блуждания о выделении нескольких групп: например, при разбиении на 11 групп, в одной гарантированно не будет "орлов". К возможным операциям добавилось инвертирование: монетку можно перевернуть изменив прежнее состояние на противоположное.
С другой стороны, можно понадеяться, что распределение будет сохраняться в больших группах, то есть выборки в 50% объёма генеральной совокупности будут репрезентативны.
Репрезентативность — соответствие характеристик выборки характеристикам популяции или генеральной совокупности в целом. Репрезентативность определяет, насколько возможно обобщать результаты исследования с привлечением определённой выборки на всю генеральную совокупность, из которой она была собрана.
В этом случае, количество "орлов" в каждой половине будет почти одинаково. Я взял да и проверил, путём моделирования, среднюю ошибку такого алгоритма. Вот тут-то всё и началось: средний результат сходился совсем не к нулю (как можно подумать сперва), и не к пяти (как можно подумать после первых прикидок). Таким образом, из одной непонятной задачи я синтезировал ещё одну - успех!
Я некоторое время помаялся, потом собрался с мыслями и вспомнил задачу про места в автобусе и гипергеометрическое распределение (не самые весёлые времена, впрочем - это другая история):
Выше приведена формула, позволяющая вычислить вероятность получить в выборке из n элементов k с признаком, если генеральная совокупность состоит из N элементов, среди которых D обладают признаком. Формула очевидна: биномиальный коэффициент в знаменателе определяет количество возможных различных исходов (сочетаний - то есть наборов, отличающихся только составом, но не порядком следования элементов). Числитель - описывает количество комбинаций элементов с признаком, для каждой из которых существует некоторое количество (описываемое вторым сомножителем) комбинаций элементов без признака.
Если в первую группу попало X1=X монеток с признаком ("орлы"), то во вторую попадёт X2=(10-X). Ошибка, в свою очередь:
Err=|X1-X2|,
Err=|X-(10-X)|,
Err=|X-10+X|,
Err=|2X-10|, X∈[0;10]
Err=|X-(10-X)|,
Err=|X-10+X|,
Err=|2X-10|, X∈[0;10]
Дело осталось за малым: посчитать вероятности для всех возможных X, сопоставить каждому X величину Err, после чего вычислить математическое ожидание.
Таблица с вероятностями X, очевидно, будет симметрична:
| X | p |
| 0 | 0,000593419672585812 |
| 1 | 0,00723682527543666 |
| 2 | 0,0379933326960434 |
| 3 | 0,113096432211476 |
| 4 | 0,211413217031676 |
| 5 | 0,259333546225529 |
| 6 | 0,211413217031679 |
| 7 | 0,113096432211476 |
| 8 | 0,0379933326960434 |
| 9 | 0,00723682527543676 |
| 10 | 0,000593419672585804 |
таблица для Err от X - тоже:
| X | Err |
| 0 | 10 |
| 1 | 8 |
| 2 | 6 |
| 3 | 4 |
| 4 | 2 |
| 5 | 0 |
| 6 | 2 |
| 7 | 4 |
| 8 | 6 |
| 9 | 8 |
| 10 | 10 |
- при вычислении вручную, можно прибегнуть к оптимизации.
Как видно - максимум вероятности соответствует X=5 (это интуитивно). Этому же X соответствует нулевая ошибка. Тем не менее, присутствие модуля в выражении Err от X, и сложная зависимость p от X порождает интересную "суперпозицию": модуль переместит оцениваемое среднее из 0 в отрезок [0;10], а непропорциональное нарастание p сместит среднее от середины отрезка ближе к нулю.
Я набросал решение для MATLAB и промоделировал ситуации с различным количеством "орлов".
Моделирование в MATLAB
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051 | N=100; %кол-во монет всего Mrk=[0 1 2 10 25 26 30 40 50]; %кол-во орлов (варианты) T=2500; %кол-во повторений каждого эксперимента Err=zeros(T,length(Mrk)); %матрица ошибок ErrM=zeros(size(Err)); %матрица средних ошибок (на каждую итерацию) AnP=zeros(length(Mrk)); %аналитические оценки средней ошибки for EID=1:length(Mrk)%цикл по экспериментам rand('twister',256); %сброс состояния ГПСЧ for Z=1:T%цикл по итерациям cns=[zeros(1,N-Mrk(EID)) ones(1,Mrk(EID))]; %создаём набор монет %(сортированный) cns=cns(randperm(N)); %перемешиваем P1=cns(1:N/2); %первая половина P2=cns(N/2+1:N); %вторая половина P1a=sum(P1); %кол-во орлов в 1-ой P2a=sum(P2); %кол-во орлов во 2-ой Err(Z,EID)=abs(P1a-P2a); %ошибка ErrM(Z,EID)=sum(Err(1:Z,EID))/Z; %средняя ошибка end %Соответствие аргументов Функции вероятности для ГГ-расп. %в matlab и на ru.wikipedia.org %HYGEPDF(X,M,K,N) %matlab <-> wiki %M - N %K - D %N - n P4n=hygepdf(0:Mrk(EID),N,Mrk(EID),N/2); %вероятности возможных исходов Err4n=abs(2*(0:Mrk(EID))-Mrk(EID)); %ошибки для данных исходов AnP(EID)=sum(P4n.*Err4n); %мат. ожидание ошибки end %Визуализация figure; for EID=1:min(9,length(Mrk)) subplot(3,3,EID); stem(Err(:,EID)); hold on; plot(ErrM(:,EID),'g','linewidth',3); plot([1 T],[AnP(EID) AnP(EID)],'r--','linewidth',3); title(['Орлов ' num2str(Mrk(EID)) '; Средняя ошибка '... num2str(AnP(EID)) ' [эксперимент. ' num2str(ErrM(T,EID)) ']']); xlabel('Итераций'); ylabel('Ошибка'); legend('эксперимент.','эксп.средняя','аналитическая'); end |
Чтобы не велосипедировать с вычислением вероятностей, я воспользовался готовой функцией
hygepdfРезультат работы ниже:
Получились очень интересные графики, изучая которые можно прийти к следующим умозаключениям:
- Аналитическая модель хорошо описывает эксперимент (см. ещё ЗБЧ).
- Есть два способа получить стабильный результат (при наличии монеток-"решек"): иметь в общей куче только 1 или 0 монеток-"орлов". Если монетка одна, она гарантированно попадёт в одну из кучек: Err=|1-0|=|0-1|=1.
- Есть только один способ (при наличии монеток-"решек") гарантированно получить нулевую ошибку: в общей куче вообще не должно быть "орлов".
- Рост корректного (см. след. пункт) числа "орлов" увеличивает среднюю ошибку, но при этом:
- Задача с нечётным количеством "орлов" априори не имеет решения. Поэтому средняя ошибка для 2n "орлов" чуть меньше, чем для (2n-1), где n∈N [?]Натуральные числа без включения нуля(сравни результаты для 26=2*13 и 25=2*13-1 монет).
- График ошибок для исходной (и других корректных) задачи квантован с шагом 2. Действительно:
Err=|2X-10|=2|X-5|, X∈[0;10]В практическом плане это означает: если монетка не попала в одну кучу, то она попадает в другую. Одновременно уменьшается количество монет в одной куче и увеличивается - в другой: суммарно оба события изменяют ошибку на 2.
Err=2X*, X*∈[0;5]
Err - чётное.
- Решение задачи не лежит в плоскости теор.вер-а.
Глава 1. Спойлеры и формализм
Опечалившись, я решил уточнить формулировку (вдруг: при пересылке что-то не скопировалось?) задачки в Интернете, и, конечно же, тут же цепанул глазом решение в поисковой выдаче (кто же думал, что он умещается в одно предложение).
Ну раз уж я взялся описывать эту задачу, то рассмотрим решение максимально подробно, а не "сделай то - потом это - готово".
Вот так выглядит дано:
Обратите внимание - мы ставим два условия:
- Общее число монет - больше одной (иначе - как их делить?).
- Число "орлов" - чётно (включая ноль).
Требуется найти разбиение на две кучки:
Так как монеты каждого типа ("орлы" и "решки") между собой неразличимы, каждое решение характеризуется (отличается от других) только количеством монет каждого типа в одной из кучек (содержимое второй кучки - очевидно).
Нетрудно заметить, что если
то есть
то существует одно решение, такое что:
Иными словами, если "решек" нет - необходимо поделить все монеты на две равные (что гарантируется) части.
Нетрудно заметить, что если
то существует
решений, таких что:
Иными словами, если "орлов" нет, то в первую кучку можно отложить от одной до половины всех (с округлением в меньшую сторону) монет, а во вторую - все оставшиеся. Остальные варианты можно получить поменяв кучки местами: в силу отсутствия нумерации кучек, эти решения не считаются отдельными.
Если рассмотренные выше оптимизации неприменимы, то проделаем следующее.
Выберем любым (так как о положении монет ничего неизвестно, для нас - случайным) образом монеты в первую кучу так, что:
Обозначим
тогда
Учитывая, что мы отобрали известное нам количество монет (см. выше):
Тогда:
Рассмотрим кучку
получаемую следующим образом:
(Вот тут и пригодится операция инвертирования монетки, описанная в Главе 0.)
Тогда получаем:
Замечаем, что:
Тогда решение:
Иными словами, необходимо случайным образом выбрать из общей кучи столько монет, сколько в ней содержится орлов. Затем, в образовавшейся кучке надо перевернуть все монетки. Всё.
Глава 2. Обобщение
Если определить операции "создание кучки" и "перевернуть все монеты в кучке" для 0 монет, то нет необходимости знать: сколько всего монет в общей куче и количество "решек".
В некоторых случаях (см. ниже), мы всё же сможем прибегнуть к оптимизации, чтобы постараться избавиться от квазикучек. Если же дополнительных требований (близость размеров кучек и т.п) у нас нет - можно использовать общий алгоритм.
Оптимизация с тривиальным решением при отсутствии "орлов" сохраняется: произвольное разбиение на две части.
Если количество "орлов" неизвестно, но всё же мы знаем, что "решек" в общей куче нет (и это всё, что мы знаем), то разбиение можно получить, последовательно откладывая монеты в 1-ую и 2-ую кучки. Хоть такой подход и можно признать косвенным (отложенным) уточнением общего количества монет, и запретить брать со стола очередную монету, если решающий не гарантирует, что она есть (при этом остаётся возможность единожды оперировать со всеми оставшимися на столе монетами).



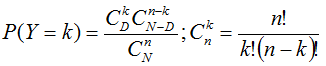

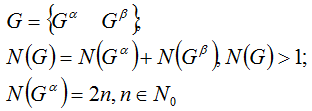
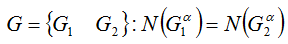
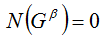
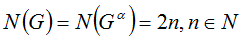
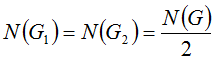
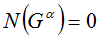
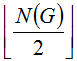
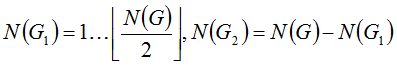
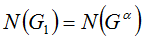
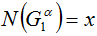
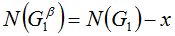
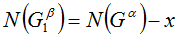
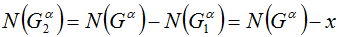
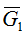

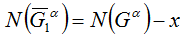

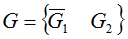

Комментарии