Траектория движения тела, брошенного под углом к горизонту

Просмотров: 2315
30 ноября 2015 года

Постановка задачи

В данной заметке я опишу алгоритм расчёта параметров траектории движения тела, брошенного под углом к горизонту и движущегося в постоянном гравитационном поле. Проблема всплывает то тут, то там: при кодировании визуализации (например, в игре "Морской бой"), при выборе искусственным интеллектом параметров стрельбы и т.п. В наиболее общей постановке задача имеет следующие условия:

Определены две точки Мира: стрелок (A) и цель (B). Определены необходимые физические параметры Мира. Во-первых: постоянная гравитация, обеспечивающая ускорение свободного падения (G); причём малые размеры сцены позволяют считать направление вектора силы притяжения одинаковым во всех точках траектории. Во-вторых: достаточно разреженная атмосфера, позволяющая пренебречь сопротивлением среды. В-третьих: начальная скорость движения тела (V).
Задача: определить угол к горизонту (alpha), под которым необходимо бросить тело, чтобы оно совершило перемещение из точки A в точку B.

Аналитические выкладки

В рамках школьного курса, обычно, решается частный случай, с совпадающими высотами точек A и B. Равенство высот упрощает вид уравнения, но, несмотря на кажущуюся рекурсию зависимости параметров, общая постановка так же имеет аналитическое решение.

Сначала распишем уравнения движения тела в проекциях на горизонтальную и вертикальную оси.

Отмечу, что какие бы координаты не были у точек A и B, при помощи переноса начала координат, условия всегда можно свести к тому, что у точки A координаты (0;0). Это упрощает запись формул, так что далее буду считать, что необходимые преобразования проведены: стрелок находится в начале координат.

x(t)=V×cos(alpha)×t
y(t)=V×sin(alpha)×t-(G/2)×(t²) .

Так как точка B должна удовлетворять уравнениям траектории, то её координаты можно подставить в уравнения.

Bx=V×cos(alpha)×T
By=V×sin(alpha)×T-(G/2)×(T²)

T - момент времени, в который тело окажется в точке B.
Из первого уравнения можно выразить время полёта:

(1) T = Bx / (V×cos(alpha)) .

Теперь подставим полученное выражение во второе уравнение (квадратные скобки здесь не несут дополнительного смысла и используются только для выделения частей уравнения):

By=V×sin(alpha)×[Bx / (V×cos(alpha))] - (G/2)×([Bx / (V×cos(alpha))]²) .

Наличие функций sin и cos одного угла, и присутствие квадрата косинуса, заставляет вспомнить тригонометрическое тождество:

cos²(x) = 1 / ( 1 + tg²(x) )

из которого можно получить:

1 / cos²(x) = tg²(x) + 1 .

Пригодится и одно из определений тангенса:

tg(x)=sin(x)/cos(x) .

Теперь, применив указанные выше тождества, получаем:

By=[Bx × (V/V) × tg(alpha)] - [(G/2) × (Bx²/V²) × (tg²(alpha)+1)].

Для удобства введём новую переменную ψ=tg(alpha):

By=[Bx × ψ] - [(G/2) × (Bx²/V²) × (ψ²+1)].

Перенесём все слагаемые в одну сторону и раскроем скобки:

[Bx × ψ] - [(G/2) × (Bx²/V²) × ψ²] - [(G/2) × (Bx²/V²)] - By = 0 .

Упорядочив по степеням ψ, получаем квадратное уравнение:

-[(G/2) × (Bx²/V²)]×ψ² + Bx×ψ - [(G/2) × (Bx²/V²)] - By = 0.

Дальнейшее решение просто до безобразия. Так как упрощений более не предвидится, то можно переходить к формулировке алгоритма.

Алгоритм

Шаг 1. Вычисляем коэффициенты квадратного уравнения и считаем дискриминант.

Решение на языке BlitzBasic
1234Local Ca#=-G*0.5*Bx*Bx/(V*V)
Local Cb#=Bx
Local Cc#=-G*0.5*Bx*Bx/(V*V)-By
Local Dis#=Cb*Cb-4*Ca*Cc

Можно оптимизировать вычисления, вычленив повторяющуюся конструкцию.

Шаг 2. Определяем количество решений или их отсутствие (ситуация с нулём решений).
Теоретически возможны три варианта:

Отрицательное значение дискриминанта. Действительных (в алгебраическом смысле) корней уравнения нет. Для нас это означает, что условия таковы, что достичь цель при заданных параметрах невозможно. В зависимости от ситуации, может помочь варьирование скорости V. Работа алгоритма завершена.

Переход от зелёного круга к красному невозможен
Положительное значение дискриминанта. Имеются два решения. Переходим к следующему шагу.

Переход от зелёного круга к красному двумя траекториями: до и после прохода наивысшей точки (обратите внимание на разность времени полёта)
Дискриминант равен нулю. Существует ровно одно решение. В рамках рассматриваемых задач такое почти недостижимо: тригонометрические функции будут порождать хвосты цифр после запятой, координаты, угол наклона или скорость нельзя будет менять непрерывно, а лишь с заданным шагом и т.п. При близких к нулю значениях, мы получим почти две сливающиеся траектории. Переходим к следующему шагу.

Переход от зелёного круга к красному почти совпадающими траекториями

Шаг 3. Находим корни уравнения.

Решение на языке BlitzBasic
12Local Psi1#=(-Cb-Sqr(Dis))/(2*Ca)
Local Psi2#=(-Cb+Sqr(Dis))/(2*Ca)

Если Вы не позаботились об отдельной обработке ситуации с одним корнем, то приведённый код вполне работоспособен. Единственный минус - без оптимизации со стороны компилятора, Вы дважды вычислите одно и тоже число. Ну и для логики принятия решения это может быть неудобно.

Шаг 4. Делаем обратную подстановку.
Получаем угол к горизонту.

Решение на языке BlitzBasic
12Local Alpha1#=ATan(Psi1)
Local Alpha2#=ATan(Psi2)

Шаг 5. Получаем время полёта (формула №1).
Не всегда этот параметр важен, но может пригодиться.

Решение на языке BlitzBasic
12Local FTime1#=Bx/(V*Cos(Alpha1))
Local FTime2#=Bx/(V*Cos(Alpha2))

Дополнительные аспекты

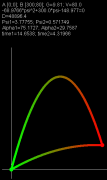
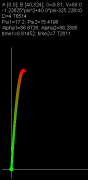
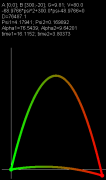
Подводных камней у алгоритма, насколько можно видеть, нет. Разумеется, при использовании его в рамках поставленной задачи. Кстати, точка B может располагаться ниже точки A:

Переход к точке, расположенной ниже

Если у Вас трёхмерная сцена, то предварительно необходимо спроецировать объекты на двумерную плоскость, в которой лежит траектория. (Некоторые аспекты этой процедуры я рассмотрю в отдельной заметке.) После этого преобразования, задача решается аналогично рассмотренной.

Запись опубликована в категориях:

Игростроение Алгоритмы и аспекты