Экспериментальные исследования прогнозирования случайного выбора человеком
Просмотров: 2157
27 апреля 2017 года
А.М. Набатчиков, Е.А. Бурлак. Экспериментальные исследования прогнозирования случайного выбора человеком // Искусственный интеллект: философия, методология, инновации. / Сборник трудов X Всероссийской конференции студентов, аспирантов и молодых учёных. Москва, МИРЭА, 27-28 апреля 2017 г. Под общей редакцией Е.А. Никитиной. – М.: Московский технологический университет (МИРЭА), 2017. – С. 42-48.
Мероприятие: Конференция "Искусственный интеллект: философия, методология, инновации." (ИИ ФМИ X)
УДК: 123:004.942
Ключевые слова: cвобода воли, детерминизм, случайный выбор, генератор случайных чисел, предсказуемость
Сайт конференции
УДК: 123:004.942
Ключевые слова: cвобода воли, детерминизм, случайный выбор, генератор случайных чисел, предсказуемость
Сайт конференции
Приведённый здесь текст публикации дополнительно содержит комментарии к опубликованному варианту. (Они разворачиваются/сворачиваются при нажатии на значок [?]
Попутно исправлены опечатки и восстановлена формула, утраченная при печати сборника.
пример пояснения
) Данные пояснения были озвучены во время доклада (или запланированы на случай возникновения вопросов у аудитории).Попутно исправлены опечатки и восстановлена формула, утраченная при печати сборника.
Аннотация
В настоящей статье рассматривается вопрос возможности предугадывания случайного выбора, совершаемого человеком. Вопрос поднимается в рамках проблемы свободной воли и детерминизма. Авторы приводят результаты экспериментальных исследований, демонстрирующих превосходство примитивных арифметических генераторов случайных чисел над способностью человека к произвольным выборам.
Введение
В своей работе «Может ли машина мыслить?» [1], Алан Тьюринг, рассматривая мнения оппонентов концепции мыслящей машины, опровергает, среди прочего, бытующее мнение о том, что «…машины не могут совершать ошибок…». Важно отметить, что речь идёт не об «ошибках функционирования», а об «ошибках вывода», совершаемых «абстрактными машинами», представляющими собой математические фикции [?]
Опечатка - функции
. Очевидно, что имитировать ошибку в вычислениях, можно добавив определённые инструкции в алгоритм. О намеренном искажении результатов случайными величинами автор упоминает далее, рассматривая проблему имитации поведения нервной системы с помощью машины с дискретными состояниями.В обоих случаях, ошибка является таковой лишь в семантическом плане для наблюдателя, в то время как для вычислительной машины нет принципиального отличия между синтаксисом инструкций генерации ошибок и синтаксисом вычисления какого-либо выражения. В связи с вышесказанным, возникает вопрос: может ли детерминированная последовательность команд порождать действительно случайные величины? Ответ на этот вопрос отрицателен [2]. В ряде задач требуется лишь имитировать случайность. Стоит отметить, что в [1] сообщается наличие у некоторых вычислителей команды генерации случайного числа. В [2] упоминается, что Тьюринг был автором метода, использующего резисторный генератор шума.
Так как наличие в природе «чистой» случайности кажется довольно ожидаемым [3], то сосредоточимся на простых арифметических генераторах псевдослучайных чисел (ГПСЧ): для работы, как правило, им нужно только одно начальное значение, на основе которого будет построена вся последовательность. В качестве начального значения часто выбирают время, так как текущее число миллисекунд в секунде или количество минут, прошедших с включения ПЭВМ – для стороннего наблюдателя – величина достаточно случайная. Данные генераторы показали свою предсказуемость [например, 4].
Исходя из сказанного выше, и в связи с увеличивающейся ролью человека в информационных и управляющих процессах [5, 6], видится интересным не столько вопрос о том, является ли данный аспект функционирования вычислительной машины её «ахиллесовой пятой», сколько вопрос: способен ли человек порождать случайную последовательность чисел, не уступающую по «качеству» хотя бы арифметическим методам генерации, ведь способности человека к творчеству «кажутся безграничными» [7]. Так как существует буквально бесконечное число критериев для проверки случайности числовой последовательности [2], конкретизируем: под «качеством» здесь мы будем понимать близость вероятности угадать n-ое число в последовательности (зная все предыдущие) к аналитической вероятности данного события для модели со случайным равномерно распределённым выбором числа из заданного диапазона. Иными словами, генератор, порождающий качественную случайную последовательность, будет обладать информационной энтропией I=log2n бит [?]
Указанная энтропия лишь иными словами описывает выбранную модель с равномерным распределением. То есть априори мы рассчитываем на худшую ситуацию, в которой появление каждого выбора равновероятно (что, забегая вперёд, апостериори необязательно). Но, в формулировке подчёркивается и наличие информации о предыдущих выборах, которое (как показано далее в статье) так же не увеличивает вероятность предсказания. Данное утверждение, иными словами, можно выразить как: автокорреляционная функция последовательности имеет вид дельта-функции Дирака. Таким образом, в нашей терминологии, чем генератор качественнее, тем "белее" шум он порождает.
.Описание экспериментов
Эксперимент проводился при помощи специально созданной программы. Испытуемому предлагалось в течение некоторого времени выбирать (при помощи манипулятора «мышь») случайным образом одну из трёх, равных по площади, прямоугольных областей на экране монитора. Проводилось два типа экспериментов: с паузой между выборами и без.
В ходе основного этапа сбора данных, испытуемым предлагалось совершить не менее 300 выборов. Вся необходимая информация фиксировалась в файле для последующего анализа.
Результаты и алгоритм предсказания
Предложенный принцип предсказания базируется на статистических свойствах последовательности выборов. В процессе создания было проверено несколько вариантов алгоритма и оставлен показавший наилучшие результаты, но не демонстрирующий негативные эффекты переобучения. Концептуально, система не использует формальные методы идентификации или обучения, так как авторы хотели получить предельно простой, но, в то же время, максимально ясный, с точки зрения семантики, алгоритм, использующий особенности человеческой интерпретации случайной последовательности.
Столбцы в таблице 1 ниже имеют следующие обозначения:
- ID – буквенный код испытуемого (Z – арифметический ГПСЧ для сравнения);
- Len – количество выборов, совершённых испытуемым за сеанс;
- T_lim – ограничение времени: минимальная пауза между выборами (мс);
- T_m – медиана времени, затрачиваемого на принятие решения (мс);
- R – результат прогнозирования: отношение количеств верных прогнозов, составленных алгоритмом, к общему количеству выборов:
.
Согласно теории вероятностей, шанс угадать загаданное число из 3 возможных равен 0,(3). В случае наличия дополнительной информации о закономерностях появления чисел в последовательности, вероятность угадывания (прогноза) возрастает.
Таблица 1
| ID | Len | T_lim | T_m | R |
| A | 331 | 0 | 117 | 0.37 |
| A | 305 | 1500 | 1584 | 0.36 |
| B | 306 | 0 | 216 | 0.44 |
| B | 300 | 1500 | 1700 | 0.44 |
| C | 333 | 0 | 466 | 0.49 |
| C | 333 | 1500 | 1765 | 0.51 |
| D | 444 | 0 | 184 | 0.34 |
| D | 302 | 1500 | 1767 | 0.67 |
| D | 306 | 1500 | 1866 | 0.49 |
| D | 333 | 1500 | 1967 | 0.48 |
| Z | 333 | 1500 | 1500 | 0.35 |
Как видно из таблицы, последовательности случайных чисел, создаваемых людьми, проигрывают в своём качестве (в значении, определённом выше) последовательности, порождённой арифметическим ГПСЧ, в котором случайности нет вовсе.
Отметим, что уменьшение медианы времени, затрачиваемого на принятие решения, свидетельствует о выборе без какой-либо концентрации над задачей [8]. Производимый таким образом шум может являться, по-видимому, результатом различных обстоятельств: существенного упрощения интерфейса ввода (в виду дефицита времени) в восприятии испытуемого (например, сужение выбора от «левый-центральный-правый» до «левый-правый») или привнесением зависимости от внешних факторов. Последнее может быть реализовано, например, путём разделения задачи выбора поля на два несвязанных процесса (случайное перемещение мыши с постоянным нажатием на клавишу) – такой метод меняет семантику выбора, добавляя к выбору человека случайные факторы в виде мышечной усталости, неравномерного хода манипулятора, посторонних предметов в рабочей области и т.п.
В любом случае, малое время принятия решения искажает условия эксперимента, делая его результаты существенно зависящими от посторонних факторов и меняя предложенную семантику выбора. Иными словами, меняется роль испытуемого в эксперименте – он становится лишь дополнительным «механическим» фильтром, окружающего его шума. В роли подобного устройства могут выступать иные электронные генераторы, реагирующие на различные шумы среды (акустические, электро-магнитные и т.п. [3]). Таким образом, человек, по сути, исключается из эксперимента.
При анализе подобного шума, качество прогнозирования, зачастую, снижается. В то же время, анализ результатов применения алгоритма к экспериментальным данным, в которых испытуемый был ограничен в частоте выбора вариантов, показывает хорошее прогнозирование поведения человека.
Применение в «камень, ножницы, бумага»
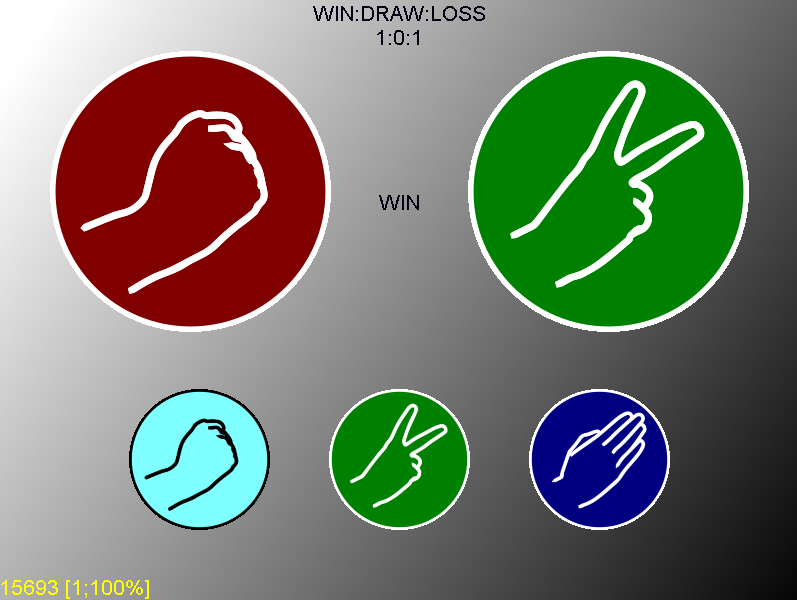
В качестве практического применения алгоритма предсказания, был разработан искусственный интеллект (ИИ) для игры в «камень, ножницы, бумага», основанный на данном алгоритме. Игровой процесс приведен на рисунке 1.
Испытуемым предлагалось сыграть как можно большее количество партий, придерживаясь (в плане выбора стратегии) своего типичного для этой игры поведения. В интерфейсе игры предусмотрен вывод рекомендации о необходимости увеличить темп принятия решения. Данная рекомендация должна пресекать попытки испытуемого идентифицировать алгоритм ИИ, затрачивая дополнительное время на обдумывание хода. Испытуемым не сообщалась истинная цель эксперимента (программа была размещена в сети Интернет, на форуме разработчиков игр и оформлена как игровой проект): предполагалось, что ИИ совершает ходы случайно.
В ходе испытаний, игроки обнаруживали слабое прогнозирование последовательностей, состоящих из повторяющихся комбинаций (например: «камень-камень-ножницы», «бумага-бумага-ножницы-ножницы-камень-камень»). Данное обстоятельство вызвано неслучайными ходами испытуемых, которые старались (по их заявлениям) подстроиться под ИИ, предназначенный для предугадывания именно случайной последовательности. Количество побед испытуемых над ИИ существенно превышало (≈7:1) количество поражений.
Для устранения эффекта, в ИИ был добавлен альтернативный блок принятия решения, выявляющий повторяющиеся комбинации, и реагирующий на них соответствующим образом (игнорируя при этом результаты работы основного алгоритма прогноза). Испытания данной версии программы показали улучшение распределения побед, поражений и ничьих (приблизилось к равномерному), при этом ≈95÷97% ходов было сделано блоком, реагирующим на комбинации, а не на случайную последовательность. Таким образом, принудить испытуемых вернуться к тактике случайного выбора хода не удалось. Впрочем, нельзя исключать того, что игроки начинали делать случайные выборы, но это приводило к возрастанию поражений и возврату к исходной тактике.
Выводы
Основываясь на полученных результатах, можно утверждать следующее.
- Даже в такой тривиальной задаче, как выбор случайных чисел, испытуемые проявляли больше предсказуемости, чем простые арифметические алгоритмы [?]Тут необходимо пояснить: что именно скрывается за этим тезисом.. Тем не менее, авторы не ставили перед собой задачу объявить поведение человека полностью прогнозируемым.
Во-первых, мы показали, что существуют алгоритмы, позволяющие прогнозировать последовательность чисел, порождаемую не только примитивным (в силу детерминированности) ГПСЧ, но и человеком. Возражение, что для успешного применения того или иного алгоритма прогноза необходимо априори знать тип генератора (то есть – человек ли перед нами), мы считаем неуместным, так как, для алгоритма генерации случайных чисел, непредсказуемость – качество, сравнимое с надёжностью для алгоритма шифрования: согласно принципу Керкгоффса, допускается, что противник может знать всё об используемой системе (алгоритмы), кроме используемых ключей (для ГПСЧ – это начальные значения генератора). Отметим, что разработанный алгоритм практически бессилен к иным ГПСЧ (не человеку), то есть, человек – аналог некоторого арифметического генератора.
Во-вторых, такая предсказуемость порождаемой человеком последовательности, при таком изобилии внешней информации, могущей выступать в качестве ключей генерации (эмоциональное состояние, предшествующие эксперименту мысли, большое количество аудиовизуальных образов и т.п.), может быть интерпретирована как примитивность используемых человеком алгоритмов.
- Ограничение времени на принятие решения меняет семантику выбора, вероятно, превращая человека в некоторый фильтр окружающего его шума (в широком смысле). При этом отмечается повышение качества (в смысле, указанном ранее) случайной последовательности.
- В присутствии некоей мотивации (влияние выбора на исход игры), человек уходит от тактики случайного выбора к тактике идентификации алгоритма, реагирующего на его выбор (что, в общем случае, не противоречит указанию «выбирать варианты случайно»). В связи с этим не удаётся использовать алгоритм прогнозирования, например, для игр, в которых выбор игрока сразу влияет на результат.
Благодарности
Авторы выражают признательность Меньшикову А. Н., за поднятую в рамках конференции ИИФМИ IX проблему свободы воли и детерминизма [9].
Авторы благодарны волонтёрам, принявшим участие в экспериментах в роли испытуемых: Andvrok, Randomize, Arton, Беляеву Андрею Алексеевичу, Маслову Дмитрию Александровичу.
Работа выполнена при поддержке РФФИ, проект № 15-08-06767
Литература
- Тьюринг А. М. Может ли машина мыслить? // Может ли машина мыслить?: Сборник. – М.: Государственное издательство физико-математической литературы, 1960. – С. 19-58.
- Дональд Кнут. Искусство программирования, том 2. Получисленные алгоритмы = The Art of Computer Programming, vol.2. Seminumerical Algorithms. — 3-е изд. — М.: «Вильямс», 2007. — С. 832.
- Жовинский В. Н. Генерирование шумов для исследования автоматических систем. М., «Энергия», 1968.
- Максимов М. Случайны ли «случайные» числа? // «Наука и Жизнь». — Издательство «Правда», 1986 г. №10. — с. 112
- Гератеволь З. Психология человека в самолёте. – М.: Издательство иностранной литературы, 1956. – 356 с.
- А.М. Набатчиков, Е.А. Бурлак. Навыки и роль человека-оператора в информационном обществе // Искусственный интеллект: философия, методология, инновации / Сборник трудов VI Всероссийской междисциплинарной конференции студентов, аспирантов и молодых учёных, г. Москва, МГТУ МИРЭА, 29-30 ноября 2012 г. // Под ред. Д.И. Дубровского и Е.А. Никтиной. Часть II (секции 4-6). – М.: МГТУ МИРЭА, 2012. – С. 81-85.
- Е.А. Бурлак, А.М. Набатчиков. Проблемы взаимодействия и распределения ролей человека и машины в динамических системах // Искусственный интеллект: философия, методология, инновации / Материалы Пятой Всероссийской конференции студентов, аспирантов и молодых учёных, г. Москва, МГТУ МИРЭА, 9-11 ноября 2011 г. Под ред. Д.И. Дубровского и Е.Д. Никитиной — М.: «Радио и Связь», 2011. – С. 244-247.
- Справочник по инженерной психологии/Под ред. Б. Ф. Ломова. – М.: Машиностроение, 1982. – 368 с., ил.
- Меньшиков А.Н. Проблема свободы воли в контексте нейроэкономики // Искусственный интеллект: философия, методология, инновации. Сборник трудов IX Всероссийской конференции студентов, аспирантов и молодых учёных. Г. Москва, МИРЭА, 10-11 декабря 2015 г. Под общей редакцией Е.А. Никитиной – М.: МИРЭА, 2015. – с. 24-27.
Файлы к скачиванию:
- Отсканированные страницы (2.9 МБ)


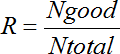
Комментарии