Концептуальная модель объекта управления при формализации деятельности человека-оператора в динамическом контуре слежения
Просмотров: 2368
Октябрь 2013 года
Себряков Г. Г., Набатчиков А. М., Бурлак Е. А. Концептуальная модель объекта управления при формализации деятельности человека-оператора в динамическом контуре слежения // Шестая Всероссийская мультиконференция по проблемам управления (30 сентября – 5 октября 2013 г.) / Материалы мультиконференции: в 4 т. – Pостов-на-Дону: Издателъство Южного федерального университета, 2013. Т.2. – С. 95-100.
Мероприятие: Шестая Всероссийская мультиконференция по проблемам управления
Сборник материалов конференции МКПУ-2013 (том 2; содержание)
Сборник материалов конференции МКПУ-2013 (том 2; содержание)
Введение
При реализации операции слежения в динамическом контуре оператор старается минимизировать ошибку между прицельной меткой и отслеживаемым символом, при этом в сознании оператора формируется образ динамического объекта, так называемая «концептуальная модель» [1]. Для того чтобы построить качественную модель человека-оператора при работе в динамическом контуре, необходимо произвести синтез концептуальной модели. Мера различия между реальным объектом управления и его концептуальной моделью может служить мерой сложности деятельности человека-оператора в динамическом контуре слежения.
Концептуальная модель
Разработку замкнутого контура двухконтурной структурно-функциональной модели деятельности человека-оператора [1] следует осуществлять на базе концептуальной модели переходных режимов. Поведение объекта в переходных режимах определяется характеристиками собственных движений. Поэтому задачу формализации концептуальной модели сформулируем следующим образом. Принимая во внимание то, что человеку присущ ряд ограничений по оценке сигналов и их производных[2, 3], делается предположение, что концептуальную модель можно формализовать в виде динамической системы второго порядка, которая оптимально описывает объект управления с позиции дисперсии ошибки между её выходом и выходом объекта управления при одинаковом воздействии.
Пусть собственные движения объекта управления описываются системой линейных дифференциальных уравнений n-ного порядка
где
x - n-мерный вектор состояний объекта;
А - постоянная квадратная матрица размера n.
Предположим, что наблюдается m-мерный вектор выходных переменных y (m<n), связанный с вектором состояния следующим соотношением:
где С - заданная матрица размера m×n.
Рассмотрим m-мерную линейную модель вида:
где В - постоянная квадратная матрица размера m.
Обозначим: y0(t) - вектор выходных переменных, соответствующий собственным движениям объекта (1) при начальном условии x0;
- вектор собственных движений модели (3) при начальном условии
Введем в рассмотрение вектор ошибки аппроксимации:
Тогда выражение:
определит интегральное квадратическое значение ошибки аппроксимации на интервале наблюдения [0,Т], который следует выбирать в зависимости от длительности переходного процесса в объекте управления.
Пусть вектор начальных условий x0 является случайной векторной величиной с нулевыми математическим ожиданием и заданной матрицей дисперсий M[x0 x0T]=θ.
Функционал
определит среднее значение дисперсии ошибки аппроксимации на интервале [0,T].
Поставим задачу найти матрицу В m-мерной модели, обеспечивающую минимум функционалу (6).
Собственные движения системы (1) при начальном условии x0 описываются равенством:
где Ф - переходная матрица состояний системы (1).
Аналогично для собственных движений модели (3) при начальном условии
имеем:
Учитывая формулы (2), (4), (7) и (8), получаем следующее выражение для оптимизируемого функционала:
Минимизируем функционал (9) по матрице Ψ(t). Необходимое и достаточное условие экстремума имеет вид:
Разрешая условие (10) относительно матрицы Ψ при невырожденной матрице СθСТ получаем:
Рассмотрим способ решения матричного уравнения (11).
Воспользуемся тем, что переходные матрицы состояний стационарных линейных систем имеют вид матричных экспонент, т.е.
Ф(t) = exp(-At), Ψ(t) = exp(-Bt).
Следствие из теоремы Кэли-Гамильтона [4] определяет представление произвольной аналитической функции от квадратной матрицы А порядка n в виде линейной комбинации n положительных целочисленных степеней матрицы А
где Δ - определитель Вандермонда;
λ1, λ2, ... , λn - собственные значения матрицы А;
Δj - определитель, получаемый из Δ подстановкой вместо элементов j-ого столбца на (f(λ1), f(λ2), ... , f(λn))T.
Используя разложение (12), матричную экспоненту, определяющую переходную матрицу состояний объекта управления, можно представить в следующем виде
где αj(t) - функция времени, зависящая от собственных чисел матрицы А(t), а именно
Ранее отмечалось, что исходя из возможностей человека-оператора оценивать состояния управляемого объекта, концептуальную модель следует искать в классе линейных систем не выше второго порядка. Поэтому разложение переходной матрицы состояний модели (3) определяется формулой:
где
λ1B, λ2B- собственные числа матрицы В = ||bij||2×2, определяемые из характеристического уравнения
|B-λBI|=λB2-(b11+b22)λB+b11b22-b21b12=0.
Проинтегрируем разложения (13) и (14) и результат подставим в (11). Приравняв элементы матриц в левой и правой частях полученного равенства, найдем систему из четырех трансцендентных уравнений с четырьмя неизвестными элементами матрицы В.
Решение этой системы численными методами не представляет принципиальных трудностей.
Апробация модели
Проведём проверку вышеизложенного метода в рамках экспериментальных исследований. В качестве проверки оценим, насколько комфортна для человека-оператора хорошо редуцируемая модель. Иными словами, покажем, что для объектов управления, концептуальная модель которых значительно отличается от самого объекта, величина дисперсии ошибки слежения будет больше.
В эксперименте рассматриваются объекты управления, описываемые передаточными функциями:
Концептуальные модели объектов, соответственно,
Проведём априорную оценку качества управления, реализуемого оператором, для каждого объекта на основе результатов редуцирования. Вычислим дисперсию ошибки для координаты при пропускании через пары передаточных функций (W1;V1) и (W2;V2) БГШ, сглаженного фильтром Wфф=10/(p2+2p+1).
EM1=0.0062, EM2=0.0079
На основе полученных данных можно утверждать, что концептуальная модель первого объекта аппроксимирует первый объект лучше, чем концептуальная модель второго объекта аппроксимирует второй объект. Следовательно, внутренне представление оператора о втором объекте управления менее точно приближает объект, а значит, качество слежения за объектом, заданным функцией W1, будет выше.
Проведём эксперимент и вычислим дисперсию ошибки слежения.
EEO1=0.1017, EEO2=1.3189.
Апостериорные данные подтверждают прогноз: объект управления, заданный функцией W2, менее удобен оператору, что приводит к большим ошибкам.
Отметим, что для обоих экспериментов траектория оператора лучше аппроксимируется выходом концептуальной модели, нежели исходного объекта управления:
EEM1=0.0776, EEM1<EEO1,
EEM2=1.2888, EEM2<EEO2.
EEM2=1.2888, EEM2<EEO2.
Приведенные выше факты показывают, что используя метод редуцирования, можно проводить априорную оценку качества управления, реализуемого человеком для данного объекта управления.
Эксперименты показывают, что чем ближе концептуальная модель к реальному объекту управления, тем лучше человек-оператор справляется с задачей слежения.
Работа выполнена при поддержке РФФИ, проект № 12-08-31290.
Литература
- Себряков Г. Г. Моделирование деятельности человека-оператора в полуавтоматических системах управления динамическими объектами // Мехатроника, Автоматизация, Управление. – М.: Новые технологии, 2010. – № 4.
- Себряков Г.Г. Экспериментальное исследование характеристик деятельности человека-оператора в динамических системах слежения и наведения летательных аппаратов // Характеристики деятельности оператора; под ред. Б.Ф. Ломова. – М.: ВНИИТЭ, 1983.
- Бурлак Е.А., Набатчиков А.М. Экспериментальные исследования деятельности человека-оператора в динамическом контуре слежения // Материалы конференции "Управление в технических, эргатических, организационных и сетевых системах" (УТЭОСС-2012). – СПб.: ГНЦ РФ ОАО "Концерн "ЦНИИ "Электроприбор", 2012. – с. 706-709.
- Kalman R., Bucy R. New results in linear filtering and prediction theory. Trans. ASME, №1, 1961.
Файлы к скачиванию:
- Отсканированные страницы (3.91 МБ)




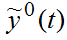
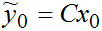





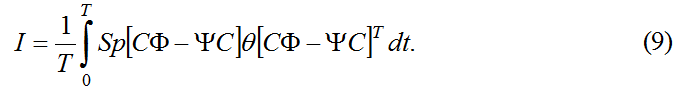
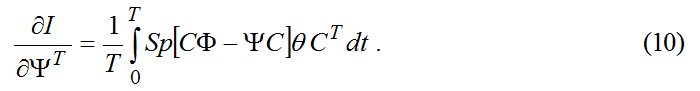
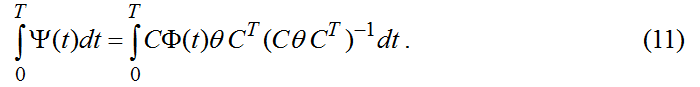
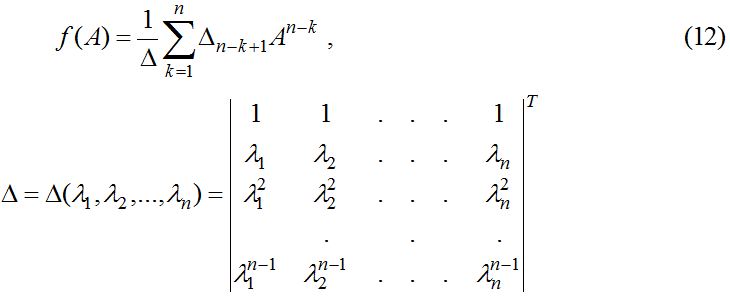
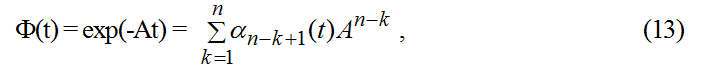
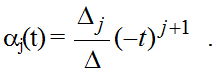
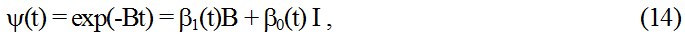
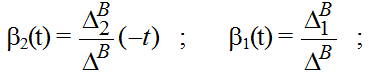
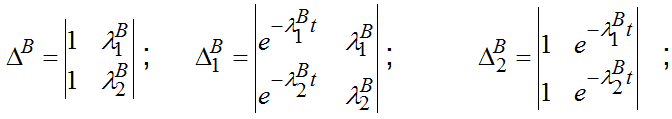
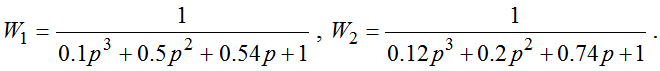
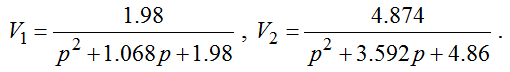
Комментарии