Экспериментальные исследования работы человека-оператора в режиме слежения при установке на максимальное быстродействие
Просмотров: 2330
2010 год
Огинский А.А., Бурлак Е.А., Набатчиков А.М. Экспериментальные исследования работы человека-оператора в режиме слежения при установке на максимальное быстродействие // Труды ГосНИИАС. ВОПРОСЫ АВИОНИКИ. – М.: ГосНИИАС, 2010. – №19. – С. 22-32.
УДК: 331.101.1:629.7
Представлены результаты исследований работы человека-оператора с различными динамическими структурами при установке на максимальное быстродействие. [?]
В процессе боевой работы летчик осуществляет прицеливание, наведение управляемых ракет, стробирование цели, т. е. выполняет операции слежения, в том числе операции совмещения прицельной марки с целью и сопровождения цели прицельной маркой. Для создания летчику наилучших условий прицеливания необходимо при проектировании учитывать зависимости процессов сопровождения и совмещения от машинной части контура слежения, в частности от его динамической структуры.
Экспериментальные исследования, результаты которых приведены далее, проведены в целях изучения деятельности человека-оператора в следящей системе при установке на возможно более быструю отработку скачка входного воздействия, что соответствует, например, стробированию цели или первоначальному совмещению прицельной марки с целью для дальнейшего сопровождения.
Работа проводилась в развитие результатов, изложенных в статье [1], где, в частности, показано, что хорошо обученные, опытные операторы работают при установке на максимальное быстродействие в соответствии с принципом максимума [2]. В предлагаемой статье изложены результаты экспериментов, проведенных с увеличенным числом операторов, причем не имевших опыта работы со следящими системами и приобретавших его в ходе экспериментов.
Эксперименты проведены на установке с органом управления (ОУ) в виде джойстика с диапазоном отклонения ±30º. Усилия на джойстике при максимальном отклонении от себя 0,455 Н, на себя 0,472 Н.
Задающий символ (цель), отрабатывающий входное воздействие и отслеживающий символ (прицельная марка) предъявлялись на мониторе с экраном размером 350х250 мм и с графическим режимом 1024х768 пикселей.
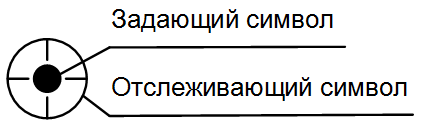
На рис. 1 задающий символ (ЗС) представлен кружком диаметром 6 пикселей (в 1 мм экрана 3,072 пикселей), отслеживающий символ (ОС) – окружностью размером 12 пикселей с двумя взаимно перпендикулярными диаметрами, имеющими разрыв в центре окружности.
Динамическая структура машинной части системы имитировалась в ПЭВМ. Там же проводилась регистрация результатов экспериментов и их математическая обработка.
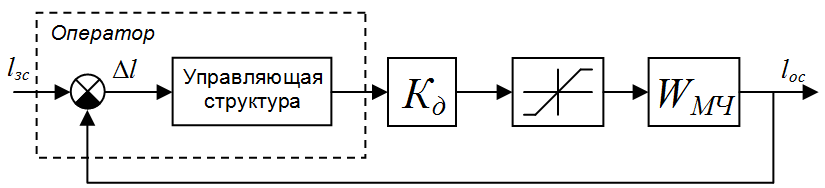
Структурная схема экспериментальной установки с оператором приведена на рис 2, где обозначено: Кд – коэффициент передачи джойстика; WМЧ – передаточная функция машинной части контура управления.
Эксперименты проведены со следующими вариантами динамической структуры машинной части WМЧ:
Величины К и Т выбирались такими, чтобы число реализаций, необходимых для адаптации операторов к заданной машинной части, не превышало 25 – 30.
Подбор репрезентативных групп операторов, адекватно представляющих всю генеральную совокупность операторов (т.е. все человечество), является непростой и, скорее всего, ненужной задачей. Более продуктивным представляется известный из математической статистики так называемый типический отбор, при котором операторы отбираются не из всей генеральной совокупности, а из каждой ее типической части [3]. Такими типическими группами операторов могут быть группы, различающиеся по возрасту, по полу, по наличию или отсутствию предварительного опыта работы в человеко-машинных системах, по профессиональной принадлежности.
В экспериментах, результаты которых приведены далее, принимали участие восемь мужчин 20 – 22 лет (студенты старших курсов). Исследовалось поведение оператора в качестве управляющего звена в контуре, представленном на рис. 2, при подаче на вход контура скачка задающего символа. Величина скачка составляла 250 пикселей. Перед оператором ставилась задача перевода отслеживающего символа в новое положение задающего символа за минимальное время с помощью джойстика.
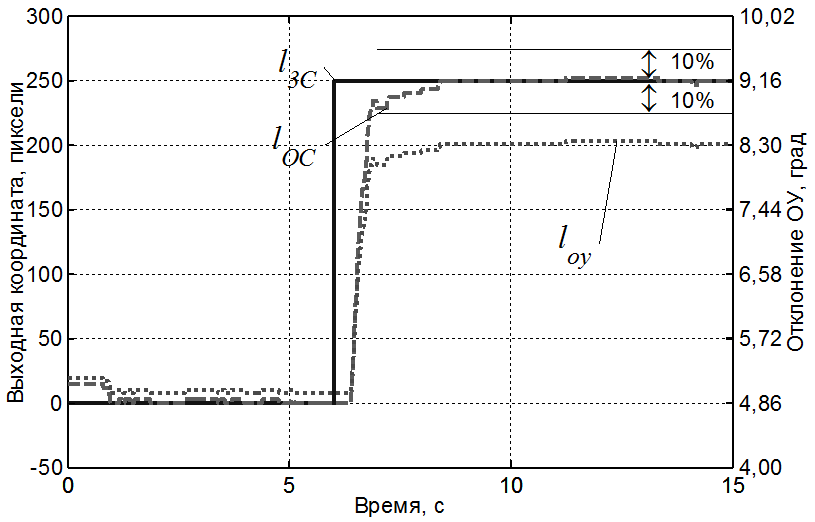
При включении в контур управления машинной части вида WМЧ1=K=1 и при установке операторов на максимальное быстродействие в первых реализациях наблюдалось небольшое перерегулирование (рис. 3), после 3 – 5 реализаций длительностью по 40 с оператор создает упреждение, компенсирующее его собственное запаздывание (обусловлено латентным периодом реакции). Переходной процесс становился монотонным и показатели деятельности стабилизировались (рис. 4). Примерно 90% величины скачка входного воздействия (с точностью до 5%) операторы отрабатывали при максимальном отклонении ОУ, затем в линейном режиме управления доводили выходную величину lос до заданного положения (снижали погрешность слежения Δl до 0).
В соответствии с принципом максимума [2], число переключений для системы с нулевым порядком характеристического уравнения равно нулю, число пребываний ОУ в крайнем положении также равно 0. Таким образом, работа оператора при отработке большого рассогласования происходит в режиме управления, оптимального по быстродействию.
При включении в контур управления машинной части вида
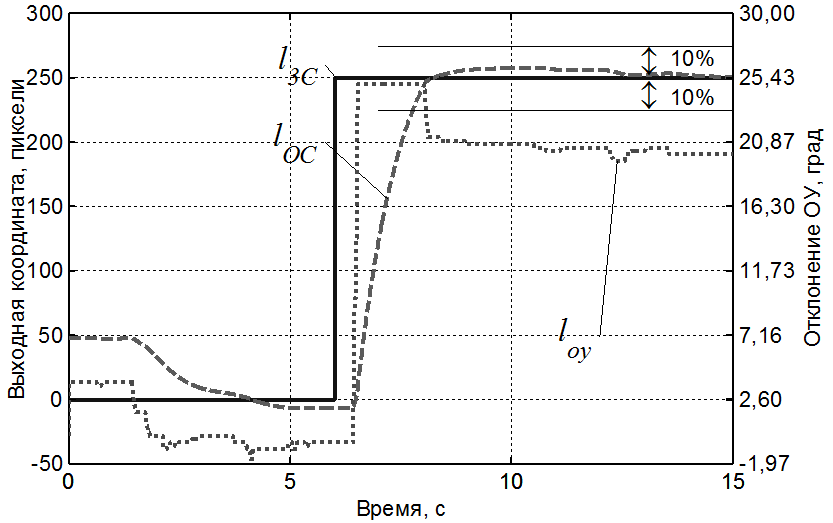
где К = 1, Т = 1 с, характеристики переходного процесса стабилизировались после 10 – 15 реализаций длительностью 40 с. Более 90% величины входного воздействия lзс отрабатывались оператором в режиме отклонения ОУ в крайнее положение. Точная доводка до заданного положения осуществлялась в режиме линейного управления. В соответствии с принципом максимума, число переключений для системы с характеристическим уравнением 1-го порядка равно нулю, число пребываний ОУ в крайних положениях равно единице.
Таким образом, оператор при отработке более 90% величины скачка входного воздействия lзс в контуре с машинной частью (МЧ) в виде апериодического звена работает в режиме оптимального быстродействия (согласно принципу максимума) с точной доводкой до заданного положения в линейном режиме оставшиеся менее 10% скачка входного воздействия. Типичный переходный процесс представлен на рис. 5.
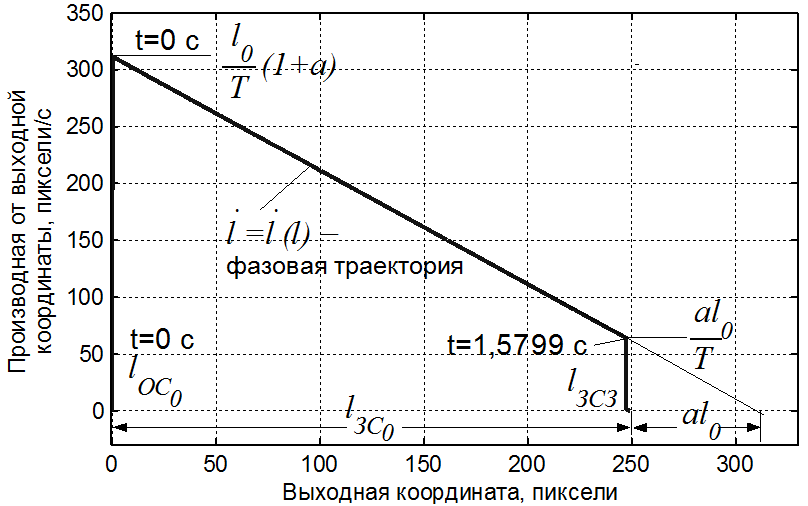
Для определения параметров оптимального переходного процесса по расчетным данным построен фазовый портрет системы с МЧ в виде апериодического звена с идеальным регулятором, оптимальным по быстродействию, а также рассчитан оптимальный переходный процесс (рис. 6, 7).
На рис. 6 и 7 обозначено:
l0 – начальное положение выходной координаты ОС;
lЗ – заданное перемещение выходной координаты МЧ, т.е. ОС;
lм – положение выходной координаты МЧ, т.е. ОС, соответствующее крайнему положению ОУ;
ЗСЗ – задающий символ заданный;
ОСЗ – отслеживающий символ заданный;
L – условное перемещение выходной координаты МЧ т.е. ОС, задаваемое оптимальным регулятором в крайним положением ОУ:
L = l0+al0 = l0 (1+a),
где a – относительное превышение крайнего положения ОУ над положением ОУ, соответствующем заданному положению выходной координаты МЧ (ОС).
Перемещение выходной координаты МЧ, т.е. ОС на величину L описывается уравнением
скорость перемещения –
время перемещения в любую точку l внутри интервала L –
уравнение фазовой траектории –
Время перемещения ОС в точку lЗ (lЗ = 0) равно
В рассматриваемом конкретном случае:
Расчетное время пребывания ОУ в крайнем положении
tз=-1*ln(0,206)=1,5799 с.
Среднее время пребывания ОУ в крайнем положении 1,54 с, среднеквадратичное отклонение 0,0826 с.
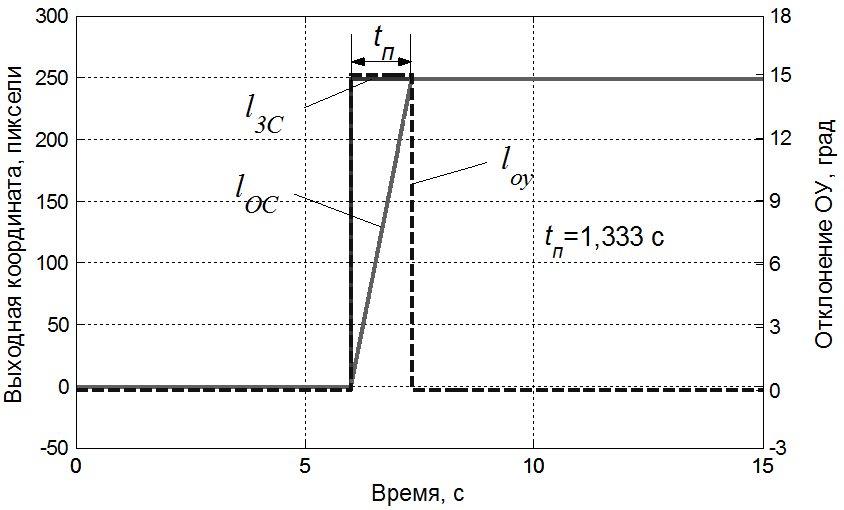
При включении в контур управления машинной части вида WМЧ3=1/p характеристики переходного процесса, так же как и при апериодическом звене, стабилизируются после 10 – 15 реализаций длительностью 40 с. Более 90% величины входного воздействия lзс отрабатываются оператором в режиме отклонения ОУ в крайнее положение. Точная доводка происходит в режиме линейного управления. В соответствии с принципом максимума число переключений равно нулю, число пребываний в крайнем положении равно единице, как и в случае МЧ в виде апериодического звена. ОУ после достижения выходной координатой положения, близкого к заданному, возвращается в положение, близкое к исходному, после чего в линейном режиме происходит точная доводка ОС до ЗС.
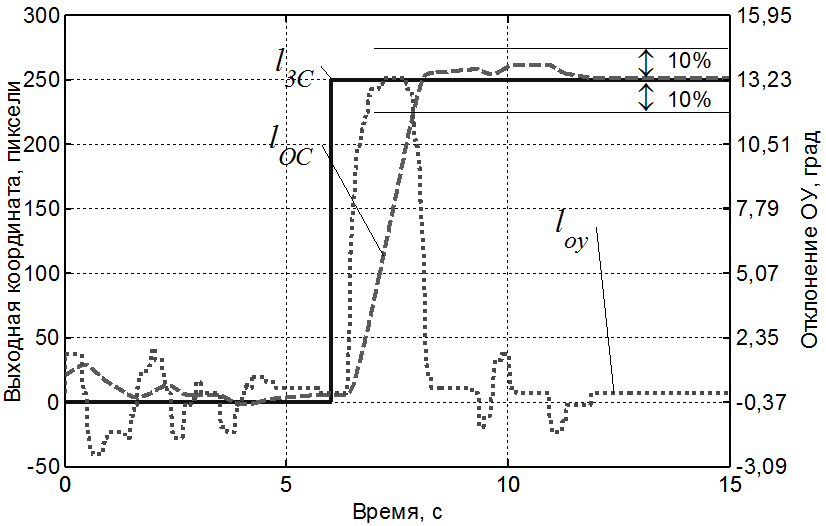
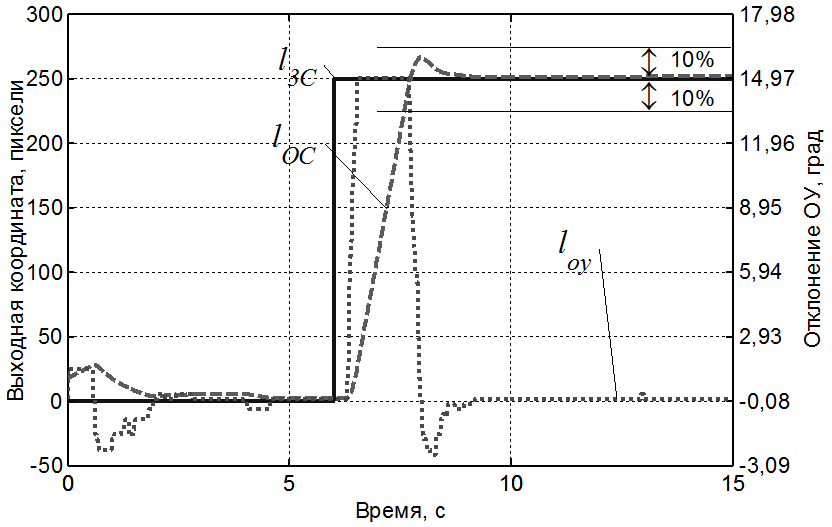
Таким образом, оператор и в случае WМЧ=1/p работает как регулирующий орган, оптимальный по быстродействию, в точном соответствии с принципом максимума для МЧ с характеристическим уравнением 1-го порядка. Типовые реализации переходного процесса представлены на рис. 8 и 9, расчетный фазовый портрет для МЧ в виде апериодического звена – на рис. 10. Оптимальный переходный процесс, построенный расчетным путем, представлен на рис. 11.
Расчетное время пребывания ОУ в крайнем положении равно 1,333 с, среднее экспериментальное – 1,459 с, среднеквадратическое отклонение – 0,121 с.
При включении в контур управления машинной части вида
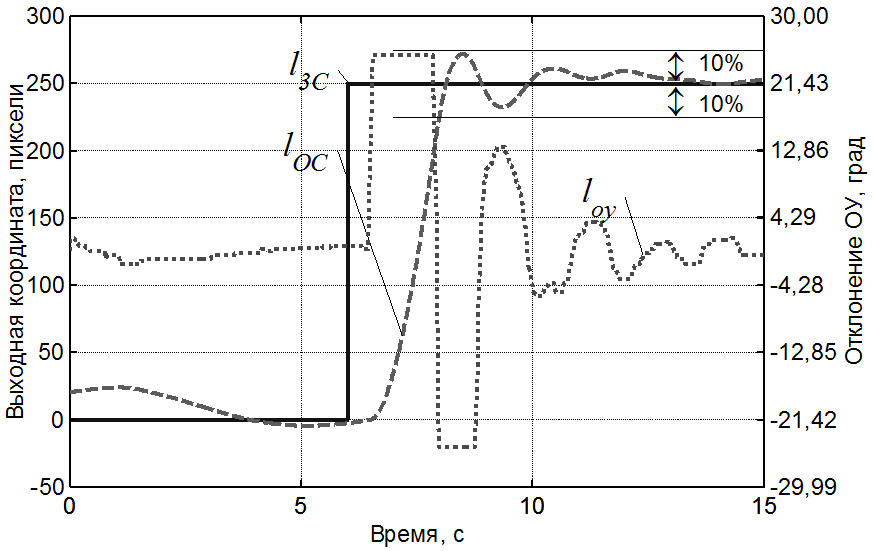
где К = 1 мм/с; Т = 1 с, при установке оператору на максимальное быстродействие все операторы для получения устойчивого контура затрачивали от 10 до 30 реализаций. Длительность каждой реализации 20 с. Затем все операторы работали в качестве линейного звена с каждой новой реализацией, снижая колебательность переходного процесса и доводя его после 20 – 40 реализаций до входа в 5%-ную трубку за время ~3 с. Никто из операторов самостоятельно не перешел в режим оптимального регулятора (по быстродействию). После элементарного ознакомления с принципом максимума операторы старались работать в качестве оптимального регулятора. Через 20 – 30 реализаций, которые следует признать тренировочными, начали получаться довольно стабильные результаты, в них джойстик в процессе управления занимал два крайних положения при одном переключении с одного крайнего положения в другое.
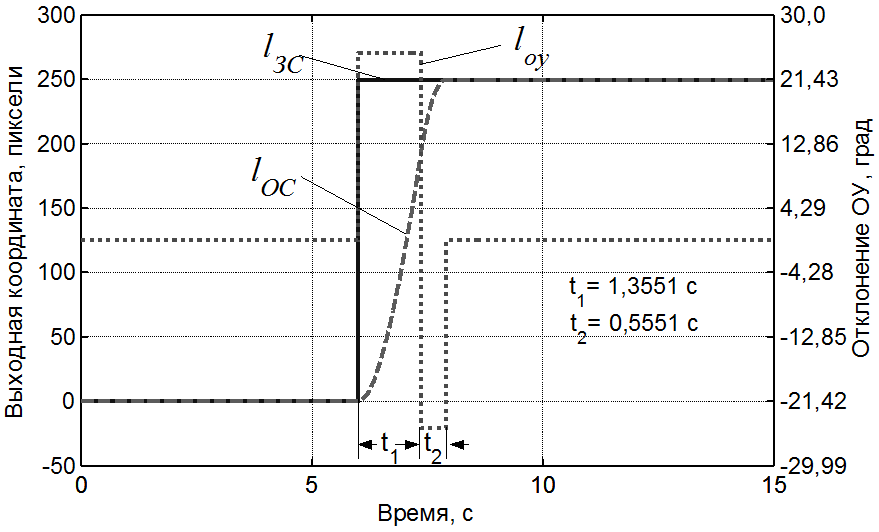
На рис. 12 представлена осциллограмма типичного переходного процесса, полученного экспериментально.
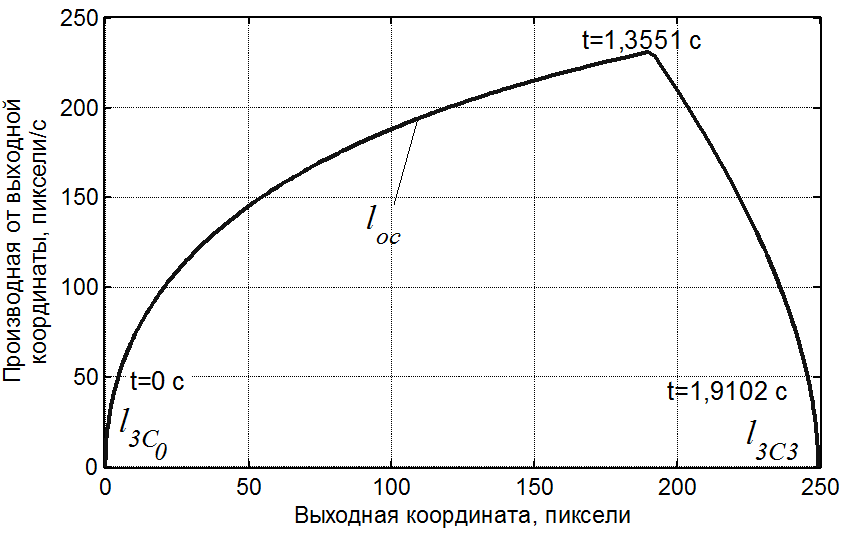
Фазовый портрет с рассчитанными по методике [4] фазовой траекторией и оптимальной линией переключения для машинной части, содержащей интегратор и апериодическое звено, представлен на рис. 13. Оптимальный переходный процесс, построенный расчетным путем, показан на рис. 14.
Расчетное время удержания ОУ в первом положении ("разгон") 1,3551 с, во втором положении ("торможение") 0,5551 с. Среднее значение (экспериментальное) пребывания ОУ в первом крайнем положении ("разгон") 1,453 с, во втором крайнем положении ("торможение") 0,855 с. Соответственно среднеквадратические отклонения – 0,0882 с и 0,017 с.
При включении в контур управления МЧ третьего порядка вида
где К = 1; T = 1 с, добиться устойчивости за 40 реализаций длительностью 20 с каждая смогли только два оператора из восьми, причем один в линейном режиме, второй – через несколько пробных, тренировочных реализаций – в режиме регулятора, похожем на оптимальный по быстродействию (два переключения и три отклонения органа управления), однако монотонности переходного процесса, а следовательно, оптимальности по быстродействию добиться не удалось. Возможно, для реализации оптимального управления следует разработать специальную методику тренировки.
Опираясь на полученные новые результаты экспериментов, целесообразно провести исследования с более широким контингентом операторов, обратив особое внимание на вопросы адаптации операторов к широкому спектру динамических структур машинной части.
Работа выполнена при поддержке РФФИ, проект № 08-08-00858-а
В процессе боевой работы летчик осуществляет прицеливание, наведение управляемых ракет, стробирование цели, т. е. выполняет операции слежения, в том числе операции совмещения прицельной марки с целью и сопровождения цели прицельной маркой. Для создания летчику наилучших условий прицеливания необходимо при проектировании учитывать зависимости процессов сопровождения и совмещения от машинной части контура слежения, в частности от его динамической структуры.
Экспериментальные исследования, результаты которых приведены далее, проведены в целях изучения деятельности человека-оператора в следящей системе при установке на возможно более быструю отработку скачка входного воздействия, что соответствует, например, стробированию цели или первоначальному совмещению прицельной марки с целью для дальнейшего сопровождения.
Работа проводилась в развитие результатов, изложенных в статье [1], где, в частности, показано, что хорошо обученные, опытные операторы работают при установке на максимальное быстродействие в соответствии с принципом максимума [2]. В предлагаемой статье изложены результаты экспериментов, проведенных с увеличенным числом операторов, причем не имевших опыта работы со следящими системами и приобретавших его в ходе экспериментов.
Эксперименты проведены на установке с органом управления (ОУ) в виде джойстика с диапазоном отклонения ±30º. Усилия на джойстике при максимальном отклонении от себя 0,455 Н, на себя 0,472 Н.
Задающий символ (цель), отрабатывающий входное воздействие и отслеживающий символ (прицельная марка) предъявлялись на мониторе с экраном размером 350х250 мм и с графическим режимом 1024х768 пикселей.
На рис. 1 задающий символ (ЗС) представлен кружком диаметром 6 пикселей (в 1 мм экрана 3,072 пикселей), отслеживающий символ (ОС) – окружностью размером 12 пикселей с двумя взаимно перпендикулярными диаметрами, имеющими разрыв в центре окружности.
Динамическая структура машинной части системы имитировалась в ПЭВМ. Там же проводилась регистрация результатов экспериментов и их математическая обработка.
Структурная схема экспериментальной установки с оператором приведена на рис 2, где обозначено: Кд – коэффициент передачи джойстика; WМЧ – передаточная функция машинной части контура управления.
Эксперименты проведены со следующими вариантами динамической структуры машинной части WМЧ:
- безынерционное линейное звено с коэффициентом передачи WМЧ1=1;
- инерционное (апериодическое) звено
где К = 1; T = 1 с;
- интегрирующее звено
где К = 1 мм/с;
- колебательное звено
где К = 1; T2 = 1,3 с2; ξ = 0,7;
- звено 2-го порядка
где К = 1 мм/с; T = 1 с;
- звено 3-го порядка вида
где К = 1; T = 1 с.
Величины К и Т выбирались такими, чтобы число реализаций, необходимых для адаптации операторов к заданной машинной части, не превышало 25 – 30.
Подбор репрезентативных групп операторов, адекватно представляющих всю генеральную совокупность операторов (т.е. все человечество), является непростой и, скорее всего, ненужной задачей. Более продуктивным представляется известный из математической статистики так называемый типический отбор, при котором операторы отбираются не из всей генеральной совокупности, а из каждой ее типической части [3]. Такими типическими группами операторов могут быть группы, различающиеся по возрасту, по полу, по наличию или отсутствию предварительного опыта работы в человеко-машинных системах, по профессиональной принадлежности.
В экспериментах, результаты которых приведены далее, принимали участие восемь мужчин 20 – 22 лет (студенты старших курсов). Исследовалось поведение оператора в качестве управляющего звена в контуре, представленном на рис. 2, при подаче на вход контура скачка задающего символа. Величина скачка составляла 250 пикселей. Перед оператором ставилась задача перевода отслеживающего символа в новое положение задающего символа за минимальное время с помощью джойстика.
При включении в контур управления машинной части вида WМЧ1=K=1 и при установке операторов на максимальное быстродействие в первых реализациях наблюдалось небольшое перерегулирование (рис. 3), после 3 – 5 реализаций длительностью по 40 с оператор создает упреждение, компенсирующее его собственное запаздывание (обусловлено латентным периодом реакции). Переходной процесс становился монотонным и показатели деятельности стабилизировались (рис. 4). Примерно 90% величины скачка входного воздействия (с точностью до 5%) операторы отрабатывали при максимальном отклонении ОУ, затем в линейном режиме управления доводили выходную величину lос до заданного положения (снижали погрешность слежения Δl до 0).
В соответствии с принципом максимума [2], число переключений для системы с нулевым порядком характеристического уравнения равно нулю, число пребываний ОУ в крайнем положении также равно 0. Таким образом, работа оператора при отработке большого рассогласования происходит в режиме управления, оптимального по быстродействию.
При включении в контур управления машинной части вида
где К = 1, Т = 1 с, характеристики переходного процесса стабилизировались после 10 – 15 реализаций длительностью 40 с. Более 90% величины входного воздействия lзс отрабатывались оператором в режиме отклонения ОУ в крайнее положение. Точная доводка до заданного положения осуществлялась в режиме линейного управления. В соответствии с принципом максимума, число переключений для системы с характеристическим уравнением 1-го порядка равно нулю, число пребываний ОУ в крайних положениях равно единице.
Таким образом, оператор при отработке более 90% величины скачка входного воздействия lзс в контуре с машинной частью (МЧ) в виде апериодического звена работает в режиме оптимального быстродействия (согласно принципу максимума) с точной доводкой до заданного положения в линейном режиме оставшиеся менее 10% скачка входного воздействия. Типичный переходный процесс представлен на рис. 5.
Для определения параметров оптимального переходного процесса по расчетным данным построен фазовый портрет системы с МЧ в виде апериодического звена с идеальным регулятором, оптимальным по быстродействию, а также рассчитан оптимальный переходный процесс (рис. 6, 7).
На рис. 6 и 7 обозначено:
l0 – начальное положение выходной координаты ОС;
lЗ – заданное перемещение выходной координаты МЧ, т.е. ОС;
lм – положение выходной координаты МЧ, т.е. ОС, соответствующее крайнему положению ОУ;
ЗСЗ – задающий символ заданный;
ОСЗ – отслеживающий символ заданный;
L – условное перемещение выходной координаты МЧ т.е. ОС, задаваемое оптимальным регулятором в крайним положением ОУ:
L = l0+al0 = l0 (1+a),
где a – относительное превышение крайнего положения ОУ над положением ОУ, соответствующем заданному положению выходной координаты МЧ (ОС).
Перемещение выходной координаты МЧ, т.е. ОС на величину L описывается уравнением
скорость перемещения –
время перемещения в любую точку l внутри интервала L –
уравнение фазовой траектории –
Время перемещения ОС в точку lЗ (lЗ = 0) равно
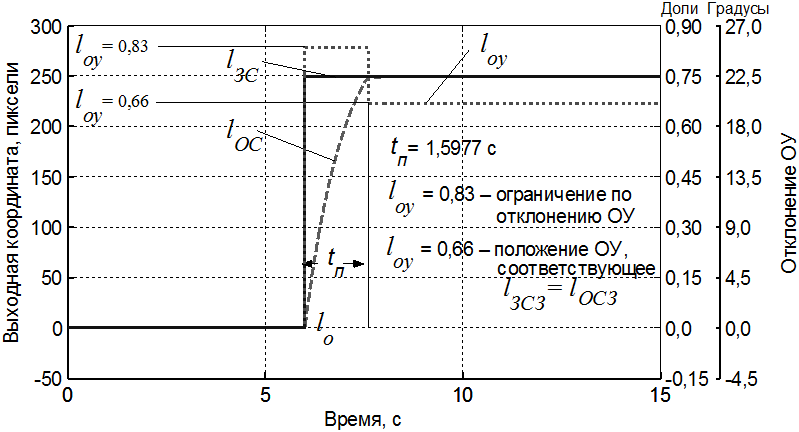
В рассматриваемом конкретном случае:
- отклонение координаты ОУ, соответствующее его крайнему отклонению, составляет 0,83;
- отклонение координаты ОУ, соответствующее заданному отклонению выходной координаты МЧ, равно 0,66;
- величина a равна
a = 0,83/0,66 - 1 = 0,26
Расчетное время пребывания ОУ в крайнем положении
tз=-1*ln(0,206)=1,5799 с.
Среднее время пребывания ОУ в крайнем положении 1,54 с, среднеквадратичное отклонение 0,0826 с.
При включении в контур управления машинной части вида WМЧ3=1/p характеристики переходного процесса, так же как и при апериодическом звене, стабилизируются после 10 – 15 реализаций длительностью 40 с. Более 90% величины входного воздействия lзс отрабатываются оператором в режиме отклонения ОУ в крайнее положение. Точная доводка происходит в режиме линейного управления. В соответствии с принципом максимума число переключений равно нулю, число пребываний в крайнем положении равно единице, как и в случае МЧ в виде апериодического звена. ОУ после достижения выходной координатой положения, близкого к заданному, возвращается в положение, близкое к исходному, после чего в линейном режиме происходит точная доводка ОС до ЗС.
Таким образом, оператор и в случае WМЧ=1/p работает как регулирующий орган, оптимальный по быстродействию, в точном соответствии с принципом максимума для МЧ с характеристическим уравнением 1-го порядка. Типовые реализации переходного процесса представлены на рис. 8 и 9, расчетный фазовый портрет для МЧ в виде апериодического звена – на рис. 10. Оптимальный переходный процесс, построенный расчетным путем, представлен на рис. 11.
Расчетное время пребывания ОУ в крайнем положении равно 1,333 с, среднее экспериментальное – 1,459 с, среднеквадратическое отклонение – 0,121 с.
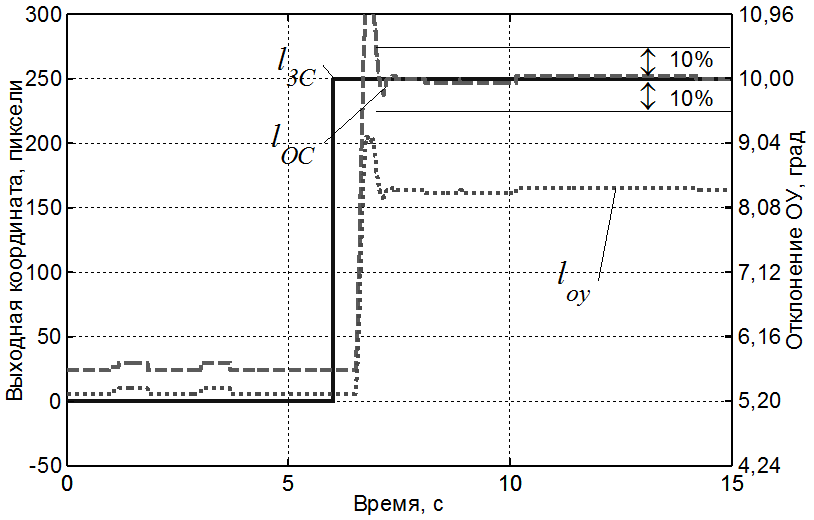
При включении в контур управления машинной части вида
где К = 1 мм/с; Т = 1 с, при установке оператору на максимальное быстродействие все операторы для получения устойчивого контура затрачивали от 10 до 30 реализаций. Длительность каждой реализации 20 с. Затем все операторы работали в качестве линейного звена с каждой новой реализацией, снижая колебательность переходного процесса и доводя его после 20 – 40 реализаций до входа в 5%-ную трубку за время ~3 с. Никто из операторов самостоятельно не перешел в режим оптимального регулятора (по быстродействию). После элементарного ознакомления с принципом максимума операторы старались работать в качестве оптимального регулятора. Через 20 – 30 реализаций, которые следует признать тренировочными, начали получаться довольно стабильные результаты, в них джойстик в процессе управления занимал два крайних положения при одном переключении с одного крайнего положения в другое.
На рис. 12 представлена осциллограмма типичного переходного процесса, полученного экспериментально.
Фазовый портрет с рассчитанными по методике [4] фазовой траекторией и оптимальной линией переключения для машинной части, содержащей интегратор и апериодическое звено, представлен на рис. 13. Оптимальный переходный процесс, построенный расчетным путем, показан на рис. 14.
Расчетное время удержания ОУ в первом положении ("разгон") 1,3551 с, во втором положении ("торможение") 0,5551 с. Среднее значение (экспериментальное) пребывания ОУ в первом крайнем положении ("разгон") 1,453 с, во втором крайнем положении ("торможение") 0,855 с. Соответственно среднеквадратические отклонения – 0,0882 с и 0,017 с.
При включении в контур управления МЧ третьего порядка вида
где К = 1; T = 1 с, добиться устойчивости за 40 реализаций длительностью 20 с каждая смогли только два оператора из восьми, причем один в линейном режиме, второй – через несколько пробных, тренировочных реализаций – в режиме регулятора, похожем на оптимальный по быстродействию (два переключения и три отклонения органа управления), однако монотонности переходного процесса, а следовательно, оптимальности по быстродействию добиться не удалось. Возможно, для реализации оптимального управления следует разработать специальную методику тренировки.
Выводы
- Операторы после тренировки отрабатывали примерно 90% скачка входного сигнала как регуляторы, оптимальные по быстродействию, строя управление в соответствии с принципом максимума, а оставшиеся относительно малые рассогласования – как линейное звено.
- Операторы при отработке 90% скачка входного воздействия имели дело с машинной частью нулевого, первого и второго порядков в соответствии с теоретическими положениями принципа максимума:
- для машинной части нулевого порядка – перевод органа управления в новое положение;
- для машинной части первого порядка:
- для апериодического звена – перевод органа управления в крайнее положение и возвращение в новое (заданное входным сигналом) положение;
- для интегрирующего звена – перевод органа управления в крайнее положение и возвращение в нулевое положение;
- для апериодического звена – перевод органа управления в крайнее положение и возвращение в новое (заданное входным сигналом) положение;
- для машинной части второго порядка – перевод органа управления в крайнее положение, затем переброс органа управления в противоположное крайнее положение, затем возврат в нулевое положение для машинной части с интегратором и в новое положение для колебательного звена.
- для машинной части нулевого порядка – перевод органа управления в новое положение;
- Часть операторов, хорошо освоивших работу с машинной частью первого порядка, переносили свой опыт на работу с машинной частью второго порядка, формируя управление в виде одного максимального отклонения органа управления. Переучивание этих операторов для работы с машинной частью второго порядка в соответствии с принципом максимума (два крайних положения и одно переключение органа управления) потребовало значительных усилий как со стороны экспериментаторов, так и со стороны этих операторов.
- При работе в системе с машинной частью третьего порядка добиться устойчивости за 40 реализаций длительностью 20 с каждая смогли только два оператора из восьми, причем один в линейном режиме, второй – через несколько пробных, тренировочных реализаций – в режиме регулятора, похожем на оптимальный по быстродействию (два переключения и три отклонения органа управления), однако монотонности переходного процесса, а следовательно, оптимальности по быстродействию добиться не удалось. Возможно, для реализации оптимального управления следует разработать специальную методику тренировки.
Опираясь на полученные новые результаты экспериментов, целесообразно провести исследования с более широким контингентом операторов, обратив особое внимание на вопросы адаптации операторов к широкому спектру динамических структур машинной части.
ЛИТЕРАТУРА
- СЕБРЯКОВ Г.Г. Экспериментальное исследование характеристик деятельности человека-оператора в динамических системах слежения и наведения летательных аппаратов/Под ред. Б.Ф. Ломова. – В сб.: Характеристики деятельности оператора. – М.: ВНИИТЭ, 1983.
- ПОНТРЯГИН Л.С. и др. Математическая теория оптимальных процессов. Изд. 4-е.– М.: Наука, Главная редакция физико-математической литературы, 1983.
- ГМУРМАН В.Е. Теория вероятностей и математическая статистика: Учеб. пособие для втузов. Изд. 5-е, перераб. и доп. – М.: Высшая школа, 1977.
- РАБИНОВИЧ Л.В. и др. Проектирование следящих систем. – М.: Машиностроение, 1969.
Файлы к скачиванию:
- Отсканированные страницы (6.01 МБ)

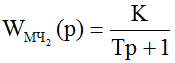
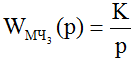
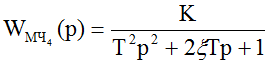
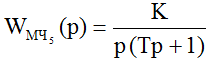
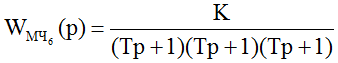
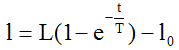
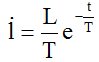
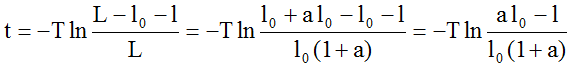
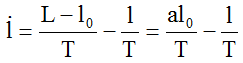
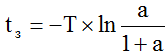
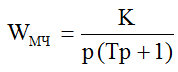
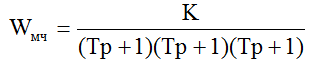
Комментарии