Анализ характеристик деятельности человека-оператора в динамическом контуре слежения
Просмотров: 2044
Ноябрь 2013 года
Набатчиков А.М., Бурлак Е.А. Анализ характеристик деятельности человека-оператора в динамическом контуре слежения // Мехатроника, автоматизация, управление. – 2013. – № 11. – С. 63-66.
ВАК
УДК: 681.5
Ключевые слова: функция когерентности, цифровая обработка сигналов, частотный метод, оконная функция, нелинейность, человек-оператор
Статья на сайте журнала
Ключевые слова: функция когерентности, цифровая обработка сигналов, частотный метод, оконная функция, нелинейность, человек-оператор
Статья на сайте журнала
Аннотация
Приведены основные сведения о функции когерентности. Рассмотрены аспекты реализации алгоритма расчета для дискретных сигналов. Показано практическое применение функции когерентности для исследования характеристик деятельности человека-оператора в системе слежения.
Введение
Когеренетность – взаимная характеристика двух сигналов – находит большое практическое применение при цифровой обработке сигналов, в частности при анализе деятельности человека-оператора (ЧО) в человеко-машинных системах слежения [1]. При реализации операции слежения, внутренняя структура ЧО может значительно изменяться, в зависимости от динамических свойств объекта управления и характеристик отслеживаемого сигнала. Ухудшение условий слежения (усложнение задачи), как правило, ведёт к увеличению нелинейности управления, реализуемого ЧО. Однако временные и статистические критерии, такие как математическое ожидание, дисперсия и др. несут в себе мало информации об изменении внутренней структуры ЧО в зависимости от степени сложности деятельности в конкретной системе. В практике инженерно-психологических исследований широкое применение находят частотные методы анализа процессов, характеризующих деятельность оператора, и в частности методы, базирующиеся на вычислении функции когерентности.
Для линейно связанных процессов функция когерентности независимо от оператора связи равна единице на всех частотах. Отличие оператора связи от линейного вызывает уменьшение значений функции. Для некоррелированных процессов функция всегда равна нулю.
Вычисление дискретной функции когерентности двух временных процессов имеет ряд особенностей. Рассмотрим их более подробно.
Необходимость покадрового усреднения
Дискретная функция когерентности имеет вид
где Sxx(fm), Syy(fm), Sxy(fm) – спектральные и взаимная спектральная плотность мощности переменных во времени сигналов x(t) и y(t); черта сверху обозначает усреднение [2]. Усреднение должно выполняться по нескольким записям сигналов, поэтому в случае наличия единственной записи сигнала необходимо разбить эту запись на кадры длиной в L отсчётов. Разделение записи длиной M отсчётов на кадры длиной L отсчётов даёт N=|_(M/L)_| кадров, где k-й кадр имеет вид
Для каждого кадра необходимо вычислить быстрое преобразование Фурье (БПФ) и спектральную плотность в соответствии с нижеприведёнными формулами:
где FFTXk* – вектор, комплексно сопряжённый вектору FFTXk и т.д.
Усреднение проводится поэлементно среди всех спектральных плотностей Sxxk, Syyk, Sxyk:
где Sxx[i], Syy[i], Sxy[i] – i-е элементы соответствующих векторов.
Итоговая характеристика вычисляется по формуле:
Причем функция (1) удовлетворяет условию
Выбор окна в соответствии с требованиями исследований
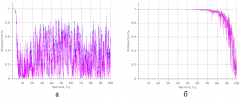
Для того чтобы избежать искажений ("растекания спектра") [3, 4], связанных с ограниченным временем наблюдения сигнала, необходимо к исходным сигналам применить некоторое сглаживающее окно, в соответствии с целями исследования. Например, на рис. 1 показаны графики функции когерентности, отличающиеся только применяемыми окнами (исследуемый сигнал один и тот же): на рис. 1, а – окно Ханна, на рис. 1, б – Хемминга.
Выбранная оконная функция может потребовать изменения величины кадра для сохранения требуемого разрешения по частоте:
где Fs – частота дискретизации сигнала, df – требуемое разрешение по частоте, ΔF0 – константа, определяемая оконной функцией.
Для использования окна необходимо осуществить свёртку сигнала с окном w:
Выбор степени перекрытия кадров
Регулируя степень перекрытия кадров, можно добиться увеличения длины кадра при сохранении их числа на той же по длине реализации сигнала. В случае, если используется перекрытие в h отсчётов, число кадров определяется как
а k-й кадр имеет вид
Чувствительность к точности моделирования сигналов
Функция когерентности чувствительна к любым незначительным погрешностям (определяемым методами решения дифференциальных уравнений, способом представления данных при регистрации и обработке), увеличивающим дискретизацию и квантование, а также изменяющим частотные характеристики реального непрерывного сигнала. На рис. 2 показано, как число знаков после десятичного разделителя (3 или 6) при регистрации сигнала влияет на конечную характеристику. В случае, когда сигнал регистрируется с тремя знаками после разделителя (рис. 2, а), характеристика не соответствует аналитическим значениям функции когерентности и содержит много шумов, а при регистрации сигнала с точностью в шесть знаков после разделителя (рис. 2, б) характеристика точнее визуализирует линейное соответствие между сигналами в области низших частот.
Результаты экспериментов
Реализованную с учётом вышеозначенных аспектов функцию удобно использовать для оценки линейности объекта, в частности, ЧО.
Были проведены две серии экспериментов на стенде по изучению работы ЧО в системах слежения [5]. В тестировании принимали участие два оператора с существенно различными операторскими навыками. Ставилась задача максимально точно отслеживать предъявляемый символ, совмещая с его изображением символ прицельной метки посредством задания управляющего воздействия через орган управления. Структурная схема контура слежения представлена на рис. 3, где: БГШ – генератор псевдослучайного белого гауссовского шума, ФФ – формирующий фильтр, М – монитор, УО – управляющий орган.
Входной сигнал (который отслеживает оператор) формировался следующим образом. Последовательность с генератора псевдослучайных чисел преобразовывалась в нормально распределённый шум и пропускалась через формирующий фильтр (ФФ). В первой серии экспериментов в качестве фильтра использовалось звено второго порядка
во второй серии – звено второго порядка
Динамика объекта управления (ОУ) описывалась звеном первого порядка
Было проведено по пять экспериментов каждого типа, по 100 с каждый с шагом дискретизации сигналов 0.005 с. При обработке использовалось окно Ханна. Длина кадра - 2048 отсчётов, с 75 %-ным перекрытием.
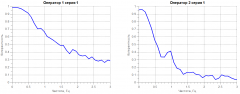
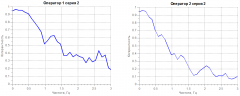
Результаты экспериментов представлены на рис. 4 и 5.
Результаты экспериментов подтверждают, что если функция когерентности исследуемых функционально связанных процессов оказывается меньше единицы, то это проявление, по крайней мере, одного из следующих случаев:
- результаты измерения содержат посторонний неконтролируемый шум;
- связь между процессами - нелинейна.
В том случае, когда задача, стоящая перед оператором, достаточно проста, как в случае первой серии экспериментов, когда входной сигнал относительно удобен оператору, ему удается реализовать близкий к линейному алгоритм управления, и функция когерентности между стимулом и реакцией человека-оператора близка к единице.
Усложнение задачи, стоящей перед оператором, как в случае второй серии экспериментов, когда входной сигнал содержит больше высокочастотных компонент, приводит к возникновению дополнительных ошибок слежения, что находит свое отражение в уменьшении функции когерентности на частотах, соответствующих указанным ошибкам. Дальнейшее усложнение задачи управления вынуждает оператора перейти к нелинейным режимам работы. Возможность такого перехода является для оператора дополнительным резервом обеспечения необходимой точности. Однако переход к нелинейным алгоритмам отработки сигналов оператором должен проявиться в изменении функции когерентности, поскольку приводит к обогащению спектра выходного сигнала системы в области высоких частот.
Заключение
Для линейно связанных процессов функция когерентности равна единице на всех частотах. Увеличение нелинейности связи уменьшает значения функции.
Вычисление функции когерентности двух цифровых сигналов сопряжено с рядом аспектов (в частности, с покадровым усреднением, выбором оконной функции и степени перекрытия кадров), которые существенно влияют на вид функции.
Из результатов экспериментов, представленных на рис. 4, 5, видно, что функция когерентности характеризует индивидуальные операторские способности человека. В обоих случаях график функции когерентности для первого оператора показывает менее крутой спад значений, чем для второго. Следовательно, первый оператор реализует управление, более близкое к линейному.
Таким образом, можно утверждать, что функция когерентности хорошо выявляет линейную связь между процессами, чувствительна к наличию посторонних шумов и нелинейностей и поэтому является удобным аппаратом исследования человеко-машинных систем.
Работа выполнена при поддержке РФФИ, проект № 12-08-31290.
Список литературы
- Себряков Г.Г. Методика исследования алгоритмов деятельности человека-оператора в динамических системах слежения // Передача, прием, обработка и отображение информации о быстропротекающих процессах: Сб. статей XXI всероссийской конференции научно-технической школы-семинара. - М.: РПА "АПР", 2010. - С. 367-373.
- Welch P. D. The Use of Fast Fourier Transform for the Estimation of Power Spectra: A Method Based on Time Averaging Over Short, Modified Periodograms // IEEE transactions on audio and electroacoustics. – 1967. – V. AU-15, №. 2, june. – pp. 70-73.
- Ханян Г.С. Некоторые аспекты конструирования и вычисления дискретной функции когерентности двух сигналов // Вестник научно-технического развития. – 2010. – №7 (35). – с. 31-35.
- Спектральный анализ на ограниченном интервале времени. Оконные функции [Электронный ресурс]. – URL: http://www.dsplib.ru/content/win/win.html (дата обращения 25.05.2013).
- Огинский А.А., Бурлак Е.А., Набатчиков А.М. Аппаратно-программный комплекс для проведения экспериментов по изучению работы человека-оператора в системах слежения // 60 научно-техническая конференция МИРЭА, Сб. тр. ч. 1, 2011 г. – с.87-91

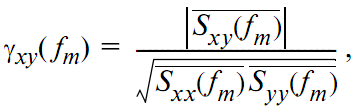
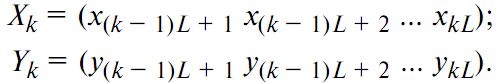
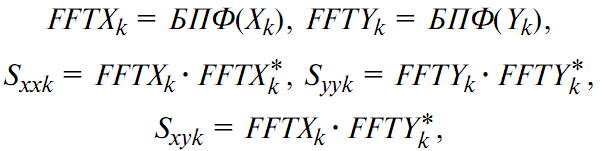
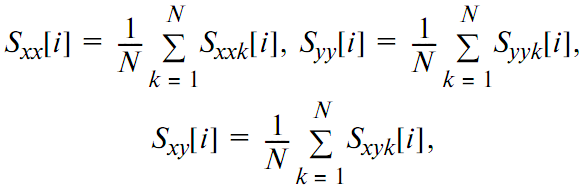
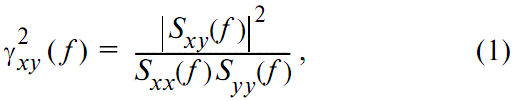
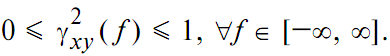

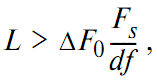
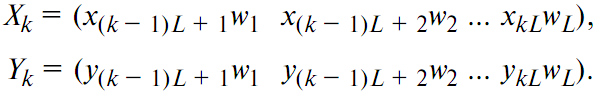
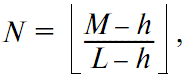
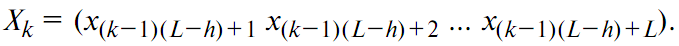

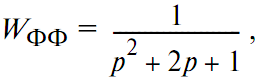
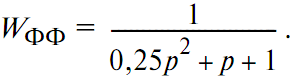
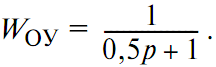
Комментарии