Змей Горыныч и Чудо-Юдо

Постановка задачи

Очень занятная и лаконичная задачка. При беглом чтении можно сразу же наступить на грабли, неверно интерпретировав условие. Затем в голову приходят излишне сложные (для 4-ого класса) решения.

Простое решение

Суть простого решения - рассуждать в категориях искомой величины, то есть времени.

Несмотря на то, что в задаче упоминается расстояние, в силу постоянной скорости полёта Змея (v=const), эта величина линейно связана с расстоянием и зависит только от затраченного времени. Последнее предложение можно опустить, так как дети, незнакомые с более искушёнными задачами, считают этот тезис априорным и воспринимают его интуитивно.

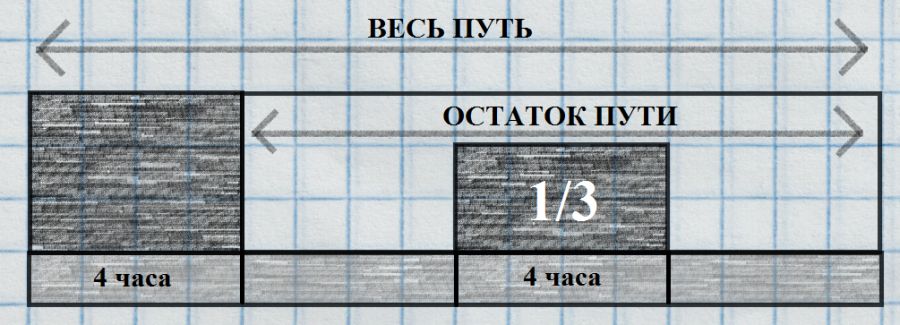
Для наглядности используем схему полёта, отмечая на ней как время так и расстояние.


Схема по пунктам:

• Змей пролетает некое расстояние, на преодоление которого затрачивает 4 часа.
  
• Известно, что если из оставшейся части пути выделить 1/3, то это расстояние будет равно уже преодолённому.
  
• На эту треть, Змей, очевидно, затратит так же 4 часа полёта.

Если схема выполнена аккуратно, то уже из неё очевидно решение:

T=4+4+4+4=16 часов

На практике, схема получится "тяп-ляп" и, без соблюдения масштаба, решение в ней не будет так хорошо заметно. Опираясь на схему и применив немного аналитики, находим решение следующим образом:

T=4+3*4=16 часов

Это выражение выводится из следующих тезисов:

• Всё время полёта складывается из уже затраченных 4 часов и времени для преодоления остатка пути.
  
• Остаток пути разбивается на три равные части, каждая из которых равна уже преодолённой.
  

Решение через дроби, переменные и пропорции

Всё расстояние можно разбить на два отрезка, равные по длине A и B.

Известно, что треть B равна A.

Тогда весь путь можно выразить как:

X=A+B=(1/3)B+B=(4/3)B

Составим пропорцию, используя выражения для длины пути:

4 часа ↔ (1/3)B
T часов ↔ (4/3)B

(4/T)=(1/3)/(4/3)

Здесь можно заметить, что формальная переменная B сократилась, подтверждая свою ненужность для вывода решения. Впрочем, переменная A просуществовала и того меньше.

T = (4*(4/3)) / (1/3) = (16/3) / (1/3) = 16 / 1 = 16 часов

Решение через дроби, переменные и функцию от времени

• Обозначим за L(t) функцию, значение которой соответствует расстоянию, преодолённому за время t.
  
• Обозначим за T искомое время, необходимое для преодоления всего пути.
  
• Обозначим за Z длину всего пути. Иными словами: L(T)=Z. (В научной статье, для этих целей запросто бы использовали переменную L_T, или даже просто L (не путать с функцией L(t)!), попутно пару раз забыв ("опустив") в доказательстве скобки при написании функции L(t).)
  

В такой нотации, текст задачи можно записать как:

L(4)=(Z-L(4))*(1/3)

На самом деле, числа ("4", "1/3") - дурновкусие и их заменили бы соответствующими обозначениями (константами).

L(4)=(1/3)*Z-(1/3)*L(4)

(4/3)*L(4)=(1/3)*Z |(*3)

4*L(4)=Z

Так как скорость полёта постоянна (V=const), функция L(t) является линейной функцией аргумента t. В таком случае, справедливо: m*L(t)=L(m*t).

4*L(4)=Z

L(4*4)=Z

L(16)=Z

Исходя из условий задачи, функция L(t) принимает значение Z (как, впрочем, и любое другое) для единственного значения аргумента, таким образом:

T=16 часов