Тест скорости выполнения функции
Просмотров: 1914
29 ноября 2016 года
Задача
Недавно на форуме была поднята тема производительности (времени выполнения) функций работы со строками. Автор вопроса интересуется поведением функции в зависимости от аргументов, передаваемых в неё. Сведений о внутреннем устройстве функции нет - сделать аналитическую оценку затруднительно. Подобное тестирование кажется тривиальным, но имеет некоторые тонкости, могущие кардинально исказить результат.
Рассмотрим аспекты подобного тестирования на примере функции
left
Организация
Раз мы проверяем зависимость времени выполнения функции от значения аргумента, то логичным кажется собрать статистику и визуализировать её при помощи графика, где по оси абсцисс будут отложены значения аргумента, а по оси ординат - затраченное время в мс.
Учитывая производительность даже не самых современных ПЭВМ, видится разумным взять диапазон побольше, а точек поменьше. Возьмём шаг изменения аргумента - 10000, а точек - 20 шт.
"Прогрев"
Всё когда-то бывает впервые. Вот операционная система уже выполняет Вашу программу, но ещё не утихла реакция на её запуск: делает какие-то выводы эвристика антивируса, происходит менеджмент памяти, что-то подгружает код, созданный компилятором для обёртки ваших высокоуровневых абстракций (что вообще представляет собой Ваша программа: байт-код для виртуальной машины, скрипт для системного интерпретатора, машинные коды?), меняется разрешение экрана и т.д. и т.п.
Не надо бросаться делать замеры производительности сразу же после запуска: она ещё не стабилизировалась. Подождите немного - прогрейте систему.
Артефакты и жеребьёвка
Если в рамках одного сеанса работы Вы хотите сравнить производительности двух функций, то какую из функций проверить первой? Если у Вас диапазон значений аргумента, то как надо перебирать значения: от меньшего к большему или наоборот? Что если какие-то флуктуации производительности затормозят первые эксперименты, исказив их результаты? А если наоборот: отсутствие взаимодействия пользователя с интерфейсом спровоцирует активацию каких-либо процессов спустя N минут теста (запуск "хранителя экрана" или процедур обслуживания)? Как долго надо "прогревать" систему? А что, если после множества выделений небольших областей памяти, запустится сборщик мусора и затормозит работу? А что если исследуемая функция умеет кешировать результаты и использовать их (очень удобно считать n!, зная только что посчитанный (n-1)!)?
Решение напрашивается следующее: вызывать нужно в случайном порядке (если речь о сравнении нескольких функций) со случайно меняющимся аргументом (если речь о зависимости от аргумента).
Критерий производительности
Если мы говорим о времени выполнения, то нам необходима информация о текущем времени. В рамках наших тестов, хорошо бы иметь функцию, возвращающую текущее время: с высокой точностью (с разрешением не больше 1 мс), с адекватным уровнем квантования результата (хотелось бы, чтобы таймер обновлялся чаще, чем пресловутые 64 раза в секунду), быстро (время работы функции несопоставимо меньше, аналогичного показателя исследуемой функции) и без каких-либо неприятных эффектов (влияние на производительность системы или, наоборот, зависимость от текущей производительности). Подбор такой функции может стать отдельной проблемой, но внимательные читатели видели заметку о том, как при помощи осциллографа, простой программки на Си++ и некоторых соображений, я обосновал адекватность использования
MilliSecs
"Моментальные" функции
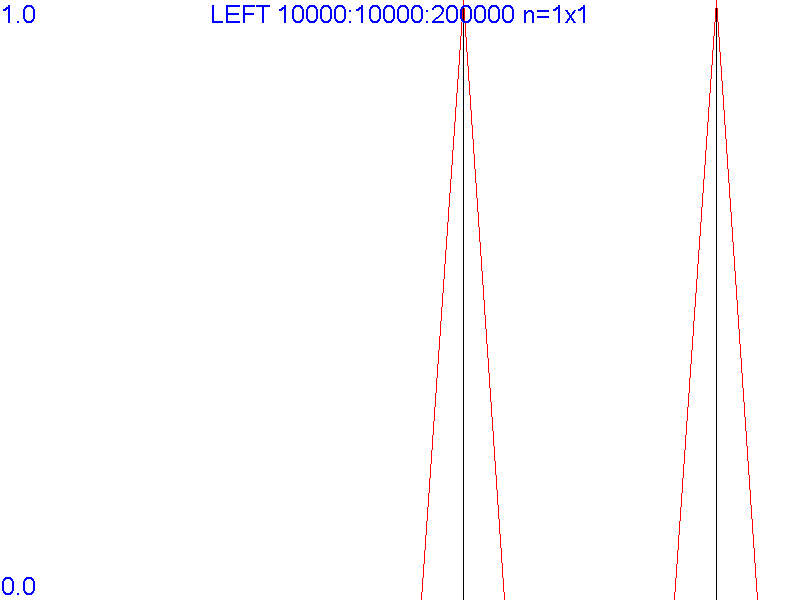
Вы прочитали изложенное выше и сразу же написали стенд для испытаний. В цикле Вы вызываете функцию, подставляя случайно изменяющийся аргумент и делая замеры времени. Результат может оказаться обескураживающим:
Если делать вывод по этому графику, то функция крайне медленно работает для двух особых значений аргумента. Эти значения не образуют какую-либо систему и не имеют аналитического обоснования.
Всё дело в том, что исследуемая функция работает слишком быстро для любого значения аргумента (из отобранных Вами). Фактически, время в 1 мс на выполнение сопоставлено тем вызовам, которые "удачно" попали на момент обновления таймера. Всё что требуется: исходя из производительности системы, подобрать некоторое количество повторений вызова функции (с фиксированным аргументом).
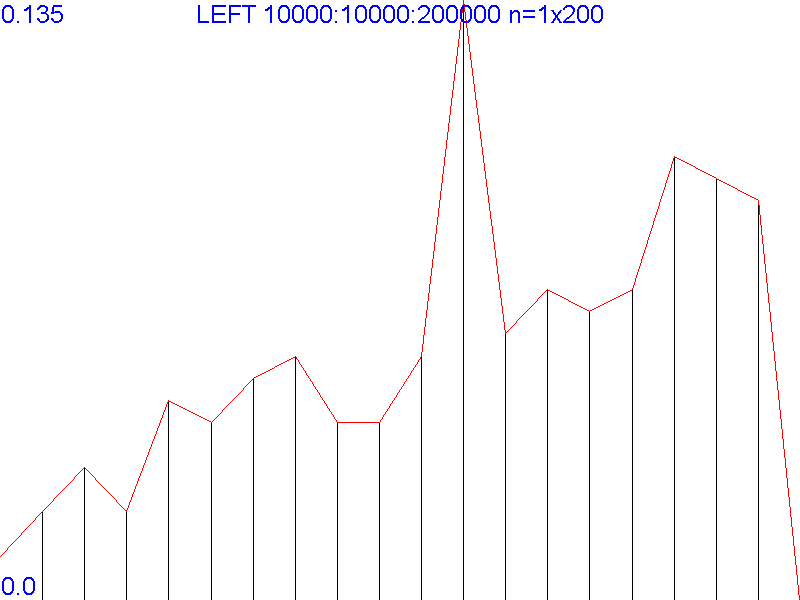
Например, будем замерять время, необходимое для двух сотен повторений функции с заданным аргументом. Полученные результаты разделим на 200, справедливо предполагая, что время выполнения функции при фиксированных условиях - постоянно.
Артефакты и жеребьёвка - развитие идеи
Как видно из рисунка выше, график получается дёрганный, хоть и с прослеживаемой тенденцией. Вероятно, выбросы соответствуют экспериментам, попавшим под провис в производительности системы. Собственно: почему мы успокоились, просто перемешав порядок подстановки значений аргумента?
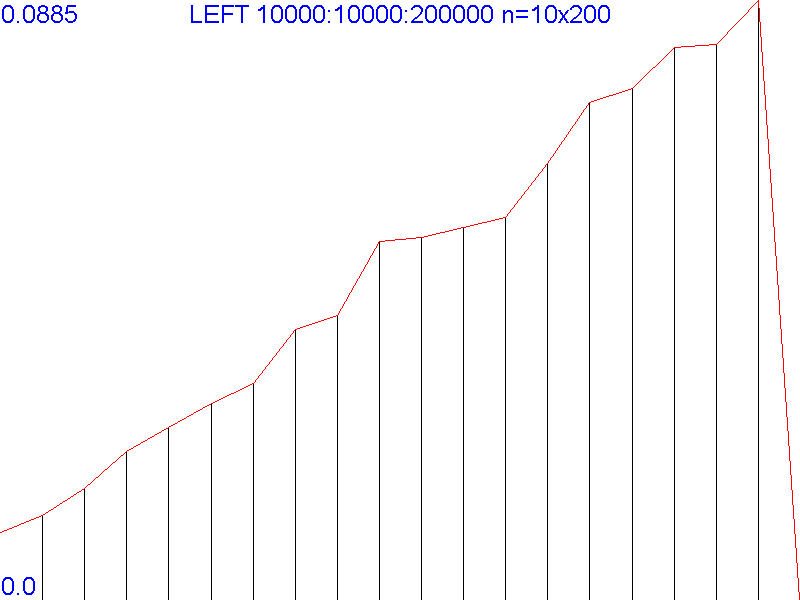
Следующая идея заключается в проведении 10 экспериментов для всего набора аргументов, причём для каждого эксперимента порядок значений будет случайно перемешан. Таким способом мы не только уравняем шансы каждого вызова попасть в удачное "окно" высокой производительности, но и сгладим (путём усреднения) броски.
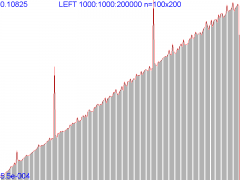
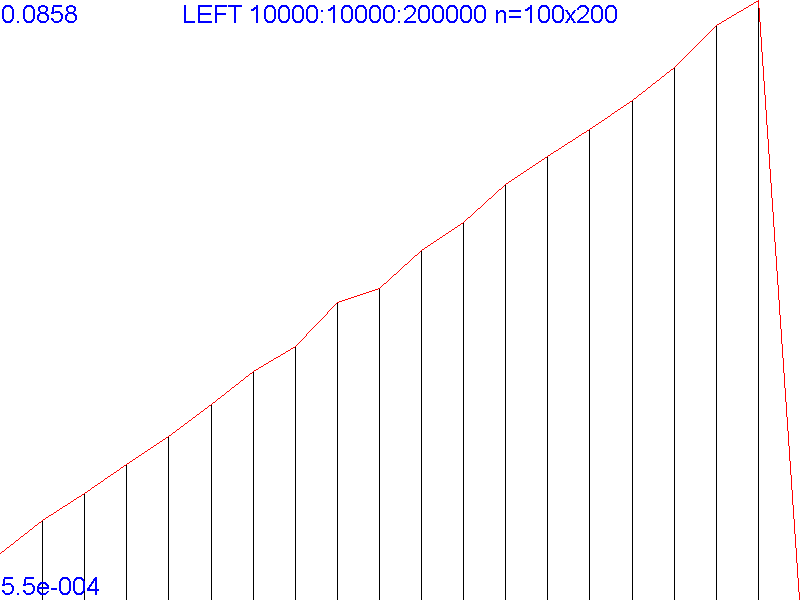
Уже вырисовывается! Увеличим число экспериментов до 100.
Выводы
Вы можете наблюдать, как время выполнения функции линейно возрастает с увеличением значений аргумента. Более того, можно вычислить тангенс угла наклона и интерполяцией получить результаты для произвольных значений, не попавших в сетку экспериментальных данных. Можно экстраполировать значения функции, но не увлекайтесь: подстрока не должна превышать строку.
Кстати, обратите внимание: на всех графиках внезапный скачок производительности для последнего значения аргумента - глобальный минимум времени выполнения. Надо полагать, что функция анализирует длину запрошенной подстроки, и когда оная достигает максимального значения, не выполняется никаких дополнительных копирований (кроме копирования результата в приёмник в точке вызова; однако не будем углубляться в эту скользкую тему).
Исходный код стенда
Стенд для проверки времени выполнения функций Blitz3D
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051525354555657585960616263646566676869707172737475767778798081828384858687888990919293949596979899100101102103104105106107108109110111112113114115116117118 | Const ExpName$="LEFT" Const ExpNum%=100 Const FuncMulti%=200 Const XStep%=10000 Const DataN%=20 Dim DataY#(DataN) Dim DataX%(DataN) Global TestStr$="" Graphics 800,600,32 SetBuffer BackBuffer() Global MyFont%=LoadFont("Arial",30) SetFont MyFont AppTitle "String..." ;подготовка тестовой строки ;конкатенация слишком дорога: сделаем паттерн.. For i%=1 To DataN TestStr=TestStr+Chr(Rand(32,126)) Next ;..и заполним им строку TestStr=String(TestStr,XStep) ;подготовка массива номеров вариантов For i%=1 To DataN DataX(i)=i Next ;цикл экспериментов For Ei%=1 To ExpNum AppTitle Str(Ei)+"/"+Str(ExpNum) RandX() ;цикл вариантов For i%=1 To DataN Local t1%=MilliSecs() For j%=1 To FuncMulti Left(TestStr,DataX(i)*XStep) Next Local t2%=MilliSecs() DataY(DataX(i))=DataY(DataX(i))+(t2-t1) Next Next ;нормировка по количеству экспериментов.. For i%=1 To DataN DataY(i)=DataY(i)/Float(ExpNum*FuncMulti) ;.. и отладочный вывод DebugLog DataY(i) Next ;график DrawGraph() Flip FlushKeys() WaitKey() FreeFont MyFont End ;Перемешивание вариантов Function RandX() ;количество перестановок - случайно от минимума до х4 Local Fact%=Ceil(DataN*Rnd(0.5,2)) ;цикл перестановок For i%=1 To Fact ;про эти формулы - см. блог nabatchikov.com (транспозиции) Local a%=Rand(1,DataN) Local b%=((a+Rand(1,DataN-1)-1) Mod DataN)+1 Local t%=DataX(a);да-да: можно оптимизировать память, сделав обмен ;в две перменные DataX(a)=DataX(b) DataX(b)=t Next End Function ;Рисование графика Function DrawGraph() ;учитывая область применения функции, ;над оптимизацией можно особо не думать. ;сотрём все белым прямоугольником Color 255,255,255 Rect 0,0,GraphicsWidth(),GraphicsHeight() ;найдём экстремумы Local max#=DataY(1) Local min#=DataY(1) For i%=2 To DataN If DataY(i)>max max=DataY(i) Else If DataY(i)<min min=DataY(i) EndIf Next ;вычислим масштбаные коэффициенты Local kx#=GraphicsWidth()/Float(DataN-1) Local ky#=GraphicsHeight()/Float(max-min) Local x1#,x2#,y1#,y2# ;отрисуем перпендикуляры для визуализации дискрет Color 0,0,0 For i=2 To DataN x1=(i-1)*kx x2=x1 y1=GraphicsHeight() y2=GraphicsHeight()-(DataY(i)-min)*ky Line x1,y1,x2,y2 Next ;соединим попарно значения для дискрет Color 255,0,0 For i=2 To DataN x1=(i-1-1)*kx x2=(i-1)*kx y1=GraphicsHeight()-(DataY(i-1)-min)*ky y2=GraphicsHeight()-(DataY(i)-min)*ky Line x1,y1,x2,y2 Next ;подпишем информацию Color 0,0,255 Text 1,GraphicsHeight()-FontHeight(),Str(min) Text 1,0,Str(max) Local Info$=Str(XStep)+":"+Str(XStep)+":"+Str(DataN*XStep)+" n="+Str(ExpNum)+"x"+Str(FuncMulti) Text GraphicsWidth()*0.5,0,ExpName+" "+Info,True,False End Function |
Размышления
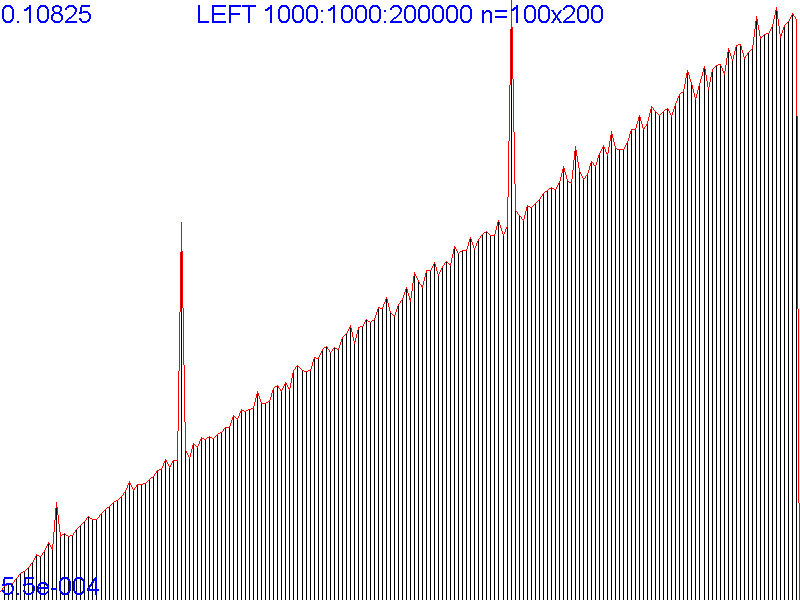
Повысим разрешение в 10 раз. Теперь тестирование длится достаточно долго, чтобы можно было успеть спровоцировать продолжительный провис производительности. Можно попробовать увеличить количество экспериментов, но чем дольше тестирование, тем больше шанс захватить момент с провисом. Можно использовать более робастные методы усреднения или сглаживать результаты (устраняя явные выбросы) различными фильтрами. В любом случае, при реализации подобных экспериментов на операционных системах, не отвечающих требованиям жёсткого реального времени, Вам не обойтись без калибровок и прикидок под конкретные обстоятельства.
Комментарии