Дифференцирование матрицы
Просмотров: 45699
04 июня 2016 года
Обновление: 1 января 2017
Обновление: 14 июля 2019
Просматривая форум, я наткнулся на своё сообщение более чем 8-летней давности. В сообщении я задавал общественности вопрос, который, в общем-то, сводился к проблеме дифференцирования матрицы по вектору. На момент написания данной заметки, ответ я так и не получил. В то же время, сейчас я не вижу принципиальных трудностей в этой задаче.
Проблема в частой для технических ВУЗ-ов ситуации: на первом курсе тебе рассказывают о физических явлениях, для описания которых необходимо понимание ротора, градиента, дивергенции, а что это за операторы и как ими пользоваться - расскажут на втором курсе.
На первый взгляд ничего непонятно: оператор дифференцирования применяется к матрицам, некоторые из которых ещё и транспонированы, дифференцирование происходит по вектору и т.п. Но не стоит паниковать: есть правила для вычисления производной и от следа матрицы, и от детерминанта произведения матриц или логарифма детерминанта матрицы - в нашем (форумном) случае всё довольно просто.
Сперва опишем общие правила дифференцирования при работе с подобными объектами.
Производная вектора по скаляру - вектор той же размерности, состоящий из производных соответствующих элементов
Производная скалярной функции f от векторного аргумента x – вектор той же размерности, что и x, равный
(То есть вектор, составленный из частных производных f по элементам вектора x.)
Производная векторной функции g размерности m по векторному аргументу x размерности n – матрица размером m×n, в которой первая строка состоит из частных производных элемента g1 по элементам вектора x и т.д.:
Следующие два результата из линейной алгебры можно получить, аккуратно проделав дифференцирование по правилам, рассмотренным ранее (тем не менее, для любопытствующих я их вывел). Эти формулы часто используются, поэтому выпишем и их:
Уточню, что первая формула (как справедливо отмечено в комментариях) справедлива только для симметричной матрицы A. В общем же случае, справа будет получено выражение (A+AT)*x. Для симметричной матрицы A, оператор транспонирования даёт саму матрицу A, что позволяет упростить выражение до указанного выше вида 2*A*x.
Собственно, возвращаясь к изначальной проблеме (вопрос на форуме):
Как продифференцировать (2.38) и получить (2.39) ?
Рассмотрим производные слагаемых из (2.38).
Для первого - всё очевидно из самого смысла производной:
Второе слагаемое (здесь воспользуемся одной из готовых формул, описанных ранее):
Третье слагаемое (воспользуемся той же готовой формулой, но предварительно немного "доработаем" выражение):
Если Вы не поняли "превращения" выше - ещё раз детальнее:
Здесь мы воспользовались свойствами транспонирования матриц:
Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.
[...]
Дважды транспонированная матрица А равна исходной матрице А.
При помощи этих свойств мы осуществили преобразования, сводящие выражение к виду, удобному для применения готовой формулы.
Четвёртое слагаемое (воспользуемся другой готовой формулой):
Соберём всё воедино и сгруппируем слагаемые:
Именно такой результат мы получили в (2.39).
Обновление: 14 июля 2019
Просматривая форум, я наткнулся на своё сообщение более чем 8-летней давности. В сообщении я задавал общественности вопрос, который, в общем-то, сводился к проблеме дифференцирования матрицы по вектору. На момент написания данной заметки, ответ я так и не получил. В то же время, сейчас я не вижу принципиальных трудностей в этой задаче.
Проблема в частой для технических ВУЗ-ов ситуации: на первом курсе тебе рассказывают о физических явлениях, для описания которых необходимо понимание ротора, градиента, дивергенции, а что это за операторы и как ими пользоваться - расскажут на втором курсе.
На первый взгляд ничего непонятно: оператор дифференцирования применяется к матрицам, некоторые из которых ещё и транспонированы, дифференцирование происходит по вектору и т.п. Но не стоит паниковать: есть правила для вычисления производной и от следа матрицы, и от детерминанта произведения матриц или логарифма детерминанта матрицы - в нашем (форумном) случае всё довольно просто.
Сперва опишем общие правила дифференцирования при работе с подобными объектами.
Производная вектора по скаляру - вектор той же размерности, состоящий из производных соответствующих элементов
Производная скалярной функции f от векторного аргумента x – вектор той же размерности, что и x, равный
(То есть вектор, составленный из частных производных f по элементам вектора x.)
Производная векторной функции g размерности m по векторному аргументу x размерности n – матрица размером m×n, в которой первая строка состоит из частных производных элемента g1 по элементам вектора x и т.д.:
Следующие два результата из линейной алгебры можно получить, аккуратно проделав дифференцирование по правилам, рассмотренным ранее (тем не менее, для любопытствующих я их вывел). Эти формулы часто используются, поэтому выпишем и их:
Уточню, что первая формула (как справедливо отмечено в комментариях) справедлива только для симметричной матрицы A. В общем же случае, справа будет получено выражение (A+AT)*x. Для симметричной матрицы A, оператор транспонирования даёт саму матрицу A, что позволяет упростить выражение до указанного выше вида 2*A*x.
Пример
Собственно, возвращаясь к изначальной проблеме (вопрос на форуме):
Как продифференцировать (2.38) и получить (2.39) ?
Рассмотрим производные слагаемых из (2.38).
Для первого - всё очевидно из самого смысла производной:
Второе слагаемое (здесь воспользуемся одной из готовых формул, описанных ранее):
Третье слагаемое (воспользуемся той же готовой формулой, но предварительно немного "доработаем" выражение):
Если Вы не поняли "превращения" выше - ещё раз детальнее:
Здесь мы воспользовались свойствами транспонирования матриц:
Транспонированное произведение матриц равно произведению транспонированных матриц, взятых в обратном порядке.
[...]
Дважды транспонированная матрица А равна исходной матрице А.
При помощи этих свойств мы осуществили преобразования, сводящие выражение к виду, удобному для применения готовой формулы.
Четвёртое слагаемое (воспользуемся другой готовой формулой):
Соберём всё воедино и сгруппируем слагаемые:
Именно такой результат мы получили в (2.39).
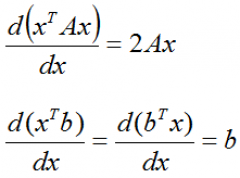
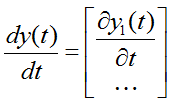
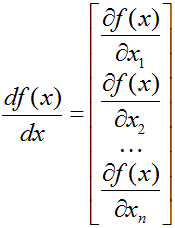
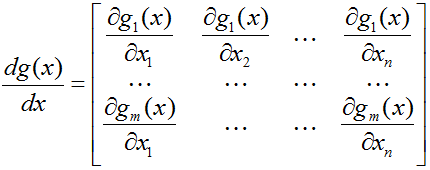
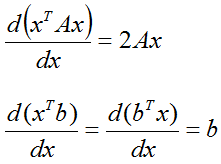
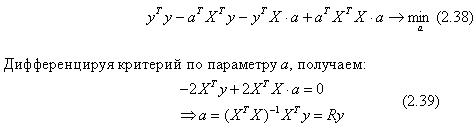
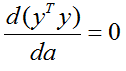
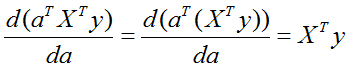
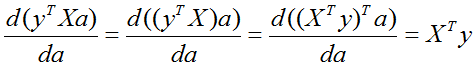
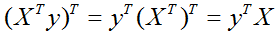

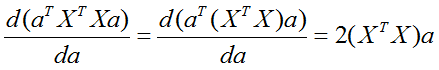

Комментарии
Rustam, в ближайшее время я выложу детальный вывод формул. Ваш комментарий окончательно убедил меня в необходимости данной заметки (у читателей возникает много вопросов по данной теме). Отвечаю на Ваш вопрос: это нормально, что оператор (в данном случае, дифференцирования) может возвращать одно и то же значение (функцию) для разных аргументов. Например, если рассмотреть функции f1(x) = (10x) и f2(x) = (10x - 8) - производные по x совпадают (10), хоть сами функции не эквивалентны. Подобным свойством могут обладать и функции: например, в квадратичной зависимости двум разным аргументам может соответствовать одно и то же значение функции.
Верно ! В общем случае там справа получим: (A+Aтранспонированное)*x.