Дифференцирование матрицы: разбираем формулы
Просмотров: 12640
14 июля 2019 года
Обновление: 8 января 2020
Обновление: 16 февраля 2020
С момента прошлой заметки по данной теме прошло много времени, но интерес к изложенному в ней не утихал. Разобравшись с основной проблемой (как, собственно, реализовать дифференцирование) читатели стали задавать вопросы о двух приведённых в тексте формулах. На этих формулах построен весь вывод, но сами они не выводятся, а сопровождены комментарием о простоте их получения при должной внимательности. Настало время.
Мне никогда не попадался вывод этих формул. Обычно, если у вас проблемы с матрицей, то надо обращаться либо к Нео, либо к Гантмахеру [?]
Подобные формулы ("Нагромождение из матриц" - "знак равенства" - "некоторая функция от матриц") выводятся стандартно: вы опускаетесь на уровень ниже - до компонент объектов (разбирая что там "под капотом" происходит), аккуратно (я бы даже сказал "осторожно") проделываете все преобразования с позиции компонент, получаете некий, более-менее конечный, результат и поднимаетесь на уровень выше (пытаясь интерпретировать формулы из компонент с позиции исходных объектов).
Отмечу, что это частный случай для симметричной матрицы A. В более же общем случае, формула имеет вид:
Для того, чтобы выражение в скобках можно было вычислить, необходимо, чтобы объекты имели следующие размеры:
Так как x - вектор, то min(m,n) = 1.
Зададимся конкретикой: пусть x - вектор-столбец, тогда n=1.
Объекты, таким образом, будут иметь вид:
Теперь, наконец-то, можно приступить к выводу. Здесь главное ничего не потерять, поэтому сперва аккуратно проделаем умножение xTA, а затем домножим результат на x.
Ожидаемо, мы получаем скаляр, зависящий от вектора. Возьмём производную скалярной функции от векторного аргумента:
Чтобы получить данное выражение, необходимо найти общий вид производной по k-ой компоненте вектора. Попробуем сгруппировать слагаемые дифференцируемого выражения по компонентам вектора, опираясь на выражение для xTAx, полученное ранее:
Очевидно, что раскрытие первых скобок даст нам x1 в квадрате с множителем a11 плюс сумму произведений x1 со всеми остальными слагаемыми внутри первых скобок. Также, x1 входит в остальные скобки по одному разу, что образует ещё слагаемые вида x1*a...*x....
Таким образом:
Если присмотреться, можно заметить закономерность (приведены множители xk: оставшаяся часть выражения скрыта за многоточием):
Теперь найти производную не составит труда:
В преобразованиях выше мы сначала объединили две сумму в одну (т.к. индексы, по которым идёт суммирование совпадают), затем первое слагаемое внесли как частный случай суммы под знак суммирования (в соответствии с индексом при x). Последняя операция изменяет условия суммирования: теперь сумма определена для всех возможных значений индекса j.
Наконец, можно заметить, что (ajk+akj) при выполнении j=k соответствует (akk+akk) = 2akk. Таким образом, выражение для первого условия покрывает и выражение для второго условия - сумму можно переписать без ветвления. Для всех компонент вектора x формула коэффициента оказалась одинакова.
Теперь несложно продолжить дифференцирование:
Осталось заметить, что левый множитель представляет собой специфическое суммирование элементов матрицы. Несложно догадаться, что компонент jk складывается с kj при сложении матрицы с её транспонированным вариантом:
Оставляя начальное и конечное выражения, получаем:
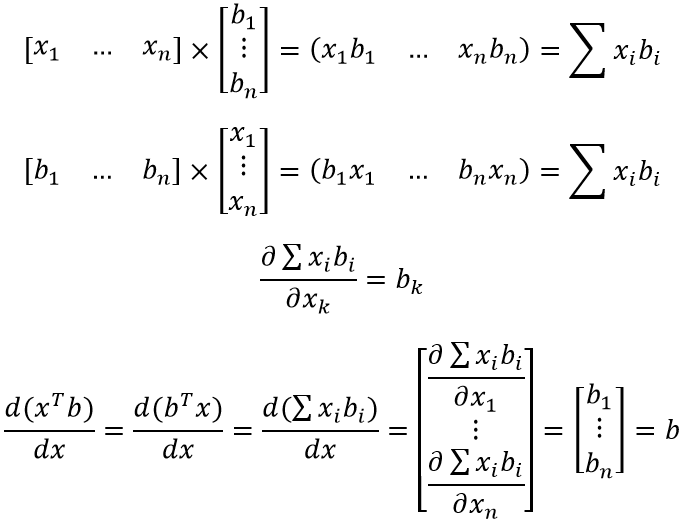
Формула (особенно, по сравнению с предыдущей) достаточна проста для восприятия и объясняется "на пальцах". xTb и bTx - это просто сумма попарного произведения компонент двух векторов (первый вектор приходится транспонировать для существования соответствующего матричного произведения). Ну и, не менее очевидное - скорость изменения от x каждой компоненты результирующего вектора определяется соответствующей компонентой вектора b.
Обновление: 16 февраля 2020
Но наибольший успех достигается с помощью такого приема: из готовой рукописи вы вырываете две страницы выкладок, а вместо них вставляете слово "следовательно" и двоеточие. Гарантирую, что читатель добрых два дня будет гадать, откуда взялось это "следствие". Еще лучше написать "очевидно" вместо "следовательно", поскольку не существует читателя, который отважился бы спросить у кого-нибудь объяснение очевидной вещи. Этим вы не только сбиваете читателя с толку, но и прививаете ему комплекс неполноценности, а это одна из главных целей.
- Н.Вансерг «Математизация».
Вместо введения
С момента прошлой заметки по данной теме прошло много времени, но интерес к изложенному в ней не утихал. Разобравшись с основной проблемой (как, собственно, реализовать дифференцирование) читатели стали задавать вопросы о двух приведённых в тексте формулах. На этих формулах построен весь вывод, но сами они не выводятся, а сопровождены комментарием о простоте их получения при должной внимательности. Настало время.
Замечание о качестве
Мне никогда не попадался вывод этих формул. Обычно, если у вас проблемы с матрицей, то надо обращаться либо к Нео, либо к Гантмахеру [?]
Ф.Р. Гантмахер "ТЕОРИЯ МАТРИЦ"
. Но в этот раз - мне никто не помог. Так что, не обессудьте: вывел как умею.Технология
Подобные формулы ("Нагромождение из матриц" - "знак равенства" - "некоторая функция от матриц") выводятся стандартно: вы опускаетесь на уровень ниже - до компонент объектов (разбирая что там "под капотом" происходит), аккуратно (я бы даже сказал "осторожно") проделываете все преобразования с позиции компонент, получаете некий, более-менее конечный, результат и поднимаетесь на уровень выше (пытаясь интерпретировать формулы из компонент с позиции исходных объектов).
Первая формула
Отмечу, что это частный случай для симметричной матрицы A. В более же общем случае, формула имеет вид:
Для того, чтобы выражение в скобках можно было вычислить, необходимо, чтобы объекты имели следующие размеры:
Так как x - вектор, то min(m,n) = 1.
Зададимся конкретикой: пусть x - вектор-столбец, тогда n=1.
Объекты, таким образом, будут иметь вид:
Теперь, наконец-то, можно приступить к выводу. Здесь главное ничего не потерять, поэтому сперва аккуратно проделаем умножение xTA, а затем домножим результат на x.
Ожидаемо, мы получаем скаляр, зависящий от вектора. Возьмём производную скалярной функции от векторного аргумента:
Чтобы получить данное выражение, необходимо найти общий вид производной по k-ой компоненте вектора. Попробуем сгруппировать слагаемые дифференцируемого выражения по компонентам вектора, опираясь на выражение для xTAx, полученное ранее:
Очевидно, что раскрытие первых скобок даст нам x1 в квадрате с множителем a11 плюс сумму произведений x1 со всеми остальными слагаемыми внутри первых скобок. Также, x1 входит в остальные скобки по одному разу, что образует ещё слагаемые вида x1*a...*x....
Таким образом:
Если присмотреться, можно заметить закономерность (приведены множители xk: оставшаяся часть выражения скрыта за многоточием):
Теперь найти производную не составит труда:
В преобразованиях выше мы сначала объединили две сумму в одну (т.к. индексы, по которым идёт суммирование совпадают), затем первое слагаемое внесли как частный случай суммы под знак суммирования (в соответствии с индексом при x). Последняя операция изменяет условия суммирования: теперь сумма определена для всех возможных значений индекса j.
Наконец, можно заметить, что (ajk+akj) при выполнении j=k соответствует (akk+akk) = 2akk. Таким образом, выражение для первого условия покрывает и выражение для второго условия - сумму можно переписать без ветвления. Для всех компонент вектора x формула коэффициента оказалась одинакова.
Теперь несложно продолжить дифференцирование:
Осталось заметить, что левый множитель представляет собой специфическое суммирование элементов матрицы. Несложно догадаться, что компонент jk складывается с kj при сложении матрицы с её транспонированным вариантом:
Оставляя начальное и конечное выражения, получаем:
ЧТД
Вторая формула
Формула (особенно, по сравнению с предыдущей) достаточна проста для восприятия и объясняется "на пальцах". xTb и bTx - это просто сумма попарного произведения компонент двух векторов (первый вектор приходится транспонировать для существования соответствующего матричного произведения). Ну и, не менее очевидное - скорость изменения от x каждой компоненты результирующего вектора определяется соответствующей компонентой вектора b.
ЧТД
Вместо выводов
Профессор, стоя у доски, был погружен в длиннейший вывод. В каком-то месте он произнес стандартную фразу "отсюда с очевидностью вытекает следующее" и написал длинное и сложное выражение, абсолютно не похожее ни на что из написанного ранее. Затем он заколебался, на его лице появилось озадаченное выражение, он что-то пробормотал и прошел из аудитории в свой кабинет. Появившись оттуда через полчаса, он с довольным видом объяснил аудитории: "Я был прав. Это, действительно, совершенно очевидно".
- Дуайт Е.Грэй «Отчеты, которые я читал... и, возможно, писал».
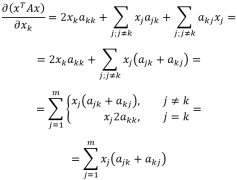

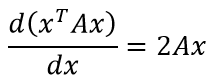
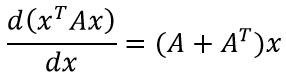
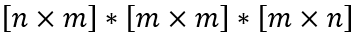


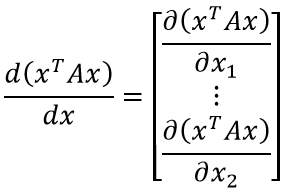
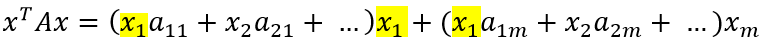
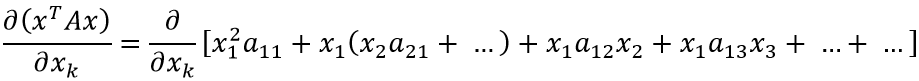
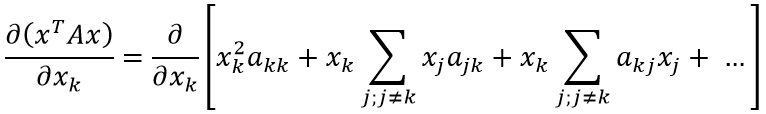
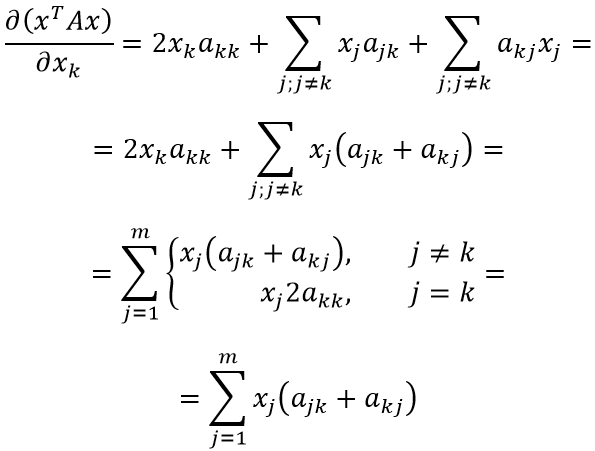
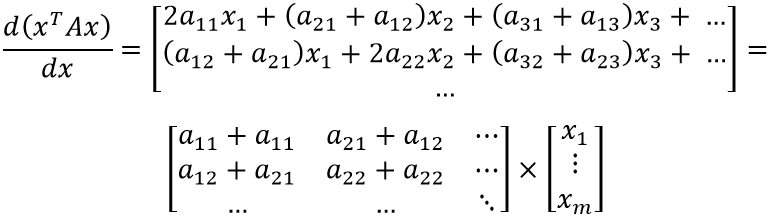
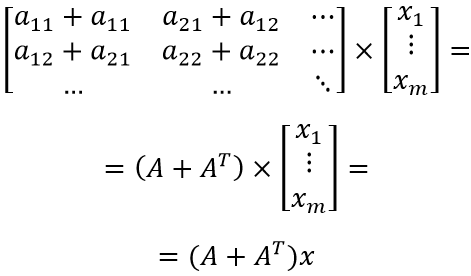
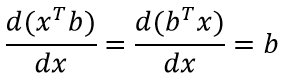
Комментарии