Задача о прямоугольной клумбе и треугольном участке
Просмотров: 1088
09 мая 2021 года
Постановка задачи
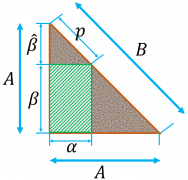
Дан участок земли, представляющий собой, в плане, равнобедренный прямоугольный треугольник. Необходимо определить максимальную площадь прямоугольного фрагмента, который возможно разместить на указанном участке.
Решение
Очевидно, что при указанной ориентации [?]
См. ниже
, клумба с максимальной площадью будет касаться гипотенузы одной из своих вершин. Тогда площадь клумбы можно выразить как параметр от положения этой вершины на гипотенузе (расстояние p):Далее, применив тривиальные соображения о геометрии фигур, получаем:
Найдём экстремум функции площади, отыскав корни уравнения "производная площади равна нулю" (значение корня не должно нарушить семантику формулы, обладающей ранее сформулированными ограничениями):
Таким образом, клумба будет занимать четверть площади квадрата со стороной A.
Открытый вопрос
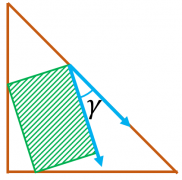
Вообще говоря, решение, относительно исходной формулировки задачи, не полное: необходимо формально обосновать, что изменение угла вращения фрагмента (клумбы) не позволит увеличить площадь по сравнению с найденным ранее значением.
Мне не удалось найти лаконичного аналитического ответа на этот вопрос. Приглашаю желающих прокомментировать.


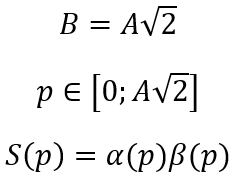
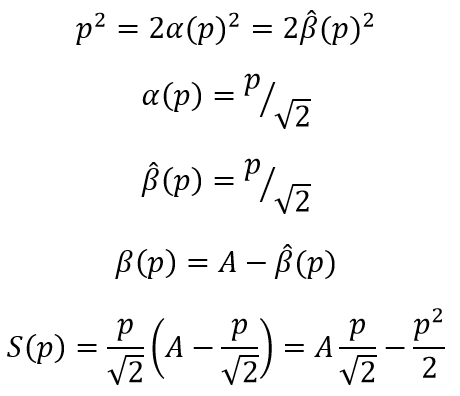
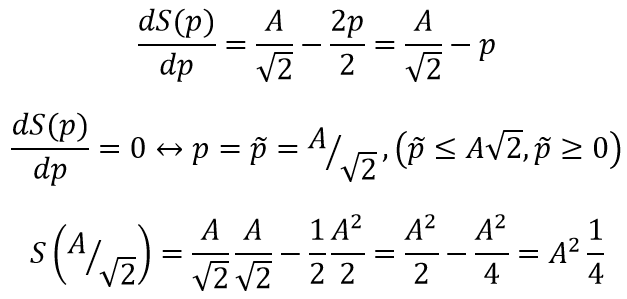
Комментарии