Синхронизация информационных потоков при полунатурном моделировании движения летательных аппаратов
Просмотров: 2729
Октябрь 2013 года
Корсун О. Н., Набатчиков А. М., Бурлак Е. А. Синхронизация информационных потоков при полунатурном моделировании движения летательных аппаратов // Электронный научно-технический журнал "Инженерный вестник". – 2013. – №10. – С. 1-16.
УДК: 629.7.018.7
Ключевые слова: полунатурный пилотажный стенд; моделирование движения летательного аппарата; синхронизация в реальном масштабе времени; интерактивное моделирование; идентификация по данным летного эксперимента; таймеры Windows
Статья на сайте журнала
Ключевые слова: полунатурный пилотажный стенд; моделирование движения летательного аппарата; синхронизация в реальном масштабе времени; интерактивное моделирование; идентификация по данным летного эксперимента; таймеры Windows
Статья на сайте журнала
Аннотация
В статье представлены результаты сравнительного анализа различных способов обеспечения синхронности информационных потоков в реальном масштабе времени в операционной системе Windows в целях построения пилотажных полунатурных моделирующих стендов. По итогам исследования предлагаются конкретные рекомендации по способам организации вычислительного процесса, обеспечивающим наилучшую согласованность моделируемых сигналов по времени.
В качестве обобщенного критерия сравнения предлагается использовать одну из наиболее сложных задач обработки полетных данных - раздельную идентификацию сил тяги и сопротивления.
Научная новизна заключается в формировании рекомендаций, обеспечивающих при моделировании в реальном масштабе времени высокую точность синхронизации сигналов, а также в разработке обобщенного критерия, позволяющего оценивать эффективность принятых решений по конечному результату.
Введение
Полунатурные моделирующие стенды являются эффективным средством создания авиационной техники. Они широко применяются для отработки систем бортового оборудования, оценивания режимов ручного и автоматизированного управления, а также для проверки алгоритмов обработки и анализа полетных данных. В таких стендах вычисления и операции ввода-вывода необходимо выполнять в реальном масштабе времени, что обусловлено наличием в контуре моделирования реального бортового оборудования и, в необходимых случаях, человека-оператора [1,2,11]. При этом одним из важнейших требований является необходимость точной синхронизации сигналов, особенно входящих в разные информационные потоки, поскольку рассогласования по времени, не соответствующие процессам в моделируемом объекте, могут приводить к сбоям в реальном оборудовании, входящем в состав стенда, искажениям характеристик ручного пилотирования, погрешностям результатов послеполетной обработки.
Традиционным решением является применения операционных систем (ОС) реального времени, например, ОС семейства Linux [3]. Этим исключается возможность использования при полунатурном моделировании широко распространенных ОС семейства Windows, которые не являются системами реального времени, поскольку не гарантируют постоянной скорости выполнения одних и тех же команд и не удовлетворяют требованиям точного выдерживания временных интервалов [3].
Между тем существующие ОС Windows имеют ряд достоинств: низкая стоимость, удобство работы, наличие многочисленных приложений, упрощающих разработку программ моделирования, а также обработку и документирование результатов [2]. Поэтому актуальным является исследование и оценка возможностей ОС Windows по обеспечению синхронности информационных потоков в реальном масштабе времени, чему и посвящена предлагаемая работа.
В целях повышения достоверности исследования выполнялись по двум существенно различным направлениям, дополняющим друг друга.
В рамках первого направления выполнялся анализ средств операционной системы, предназначенных для синхронизации информационных потоков, оценивались их возможности и порядок функционирования. При этом рассматривались функции определения текущего времени, возможности по стабилизации временных интервалов, а также способы распараллеливания вычислений и операций ввода-вывода. Проведенные исследования позволили сформулировать ряд рекомендаций по организации вычислительного процесса в реальном масштабе времени. Однако в силу сложности и многосвязности процессов функционирования операционной системы при всех вариантах сохраняются элементы неопределенности, оказывающие влияние на результаты моделирования.
Поэтому в рамках второго направления был предложен обобщенный критерий оценивания эффективности синхронизации. Для этого была выбрана одна из наиболее сложных задач обработки данных летных испытаний - раздельная идентификация сил тяги и сопротивления [4, 5]. Задача относится к классу некорректных в смысле А.Н. Тихонова [6] и имеет высокую чувствительность к погрешностям входных данных. В качестве меры точности синхронизации предлагается принять погрешности оценок, например, силы тяги, вычисленные по результатам моделирования на полунатурном стенде. Если какой-либо вариант синхронизации обеспечивает пренебрежимо малые погрешности идентификации, то, в силу выбора тестовой задачи, можно с высокой вероятностью предполагать, что такая синхронизация не вносит погрешностей при оценивании большинства алгоритмов обработки полетных данных.
1 Анализ средств синхронизации операционной системы
Функции запроса времени. Как отмечалось выше, ОС семейства Windows не гарантируют точное соответствие времени, возвращаемого соответствующими системными функциями, реальному времени. Кроме того, разные функции имеют разный шаг квантования, а их вызов сопряжён с затратами процессорного времени, что также увеличивает погрешности измерений. При этом отсутствуют четкие рекомендации по выбору метода измерения времени. В результате выбор программистом той или иной функции является зачастую следствием привычки или недостаточной осведомлённости.
Рассмотрим четыре наиболее популярных в программах на языке C++ способа получения оценок текущего времени с точностью до долей секунды (в других языках можно найти аналоги данных функций):
- Функция (далее, для краткости, CLK). Функция возвращает количество тактов; для получения частоты тактов нужно использовать макроопределение
clock()[16].CLOCKS_PER_SEC
- Функция (далее GTC). Функция возвращает текущее системное время в миллисекундах.
GetTickCount
- Функция (далее TGT). Функция возвращает текущее системное время в миллисекундах. Для работы используется библиотека мультимедиа API (Application Programming Interface), обеспечивающая интерфейс программирования приложений в ОС Windows -
timeGetTime
.winmm
- Функция (далее QPC). Функция возвращает текущее системное время в тактах; для поучения частоты тактов нужно вызвать функцию
QueryPerformanceCounter
.QueryPerformanceFrequency
Основанная трудность исследования заключается в том, что для определения характеристик качества функций времени (время работы и точность измерений) необходимо использовать сами исследуемые функции, то есть заранее знать искомые характеристики. Избавиться от рекурсии возможно путём вовлечения в исследования независимого устройства, позволяющего произвести точные измерения времени. Имея метод измерения временного интервала, на протяжении которого функция не меняет своё значение, мы можем (приняв допущение, что частота вызова функции стабильна и равна средней частоте) каждому её изменению сопоставить значение реального времени. Таким образом, если среднее время изменения значения функции составляет dtf, мы можем считать, что N-ое значение функция примет в момент времени dtf*N.
Для проведения экспериментов по оценке характеристик вышеперечисленных функций использовалась ПЭВМ с процессором Intel Pentium 4 (два ядра с тактовой частотой 3ГГц) и объёмом оперативной памяти 1 ГБ. К параллельному (LPT) порту ПЭВМ, к контакту разъема, соответствующему младшему биту данных, был подключён щуп осциллографа С1-112 [17].
Исследования проводились путём изменения настроек программы, установленной на ПЭВМ и управляющей состоянием LPT-порта [21, 22, 23], и анализа показаний осциллографа.
При наступлении заданного события (условия различались в разных экспериментах), программа увеличивала значение, выводимое на порт. Так как значения N и N+1 всегда отличаются младшим битом (в том числе, в случае переполнения счётчика), то наступление события приводило к изменению уровня сигнала на экране осциллографа, и формированию меандра. Подбор параметров работы осциллографа позволял с высокой точностью определить среднюю частоту наступления события. Программа имела возможность применить операцию битового сдвига значения счётчика на k разрядов, что позволяло изменить частоту наступления события в 2k раз. Последнее позволяло провести измерения при разных масштабах развертки осциллографа по времени для минимизации погрешности измерений.
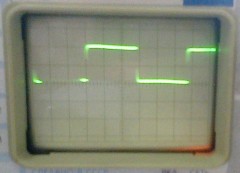
Пример сигнала, получаемого на экране осциллографа, приведен ниже.
Кроме того, программа имела возможность сохранять регистрируемые сигналы в энергонезависимую память для последующей обработки.
Рассмотрим результаты экспериментов по определению основных свойств каждой исследуемой функции. В эксперименте минимальная дискретность изменения времени составляла 0,04 мс, что соответствовало частоте выполнения цикла на данной ПЭВМ без дополнительной нагрузки на процессор – 25 кГц.
Функция CLK практически не тратит процессорное время на свой вызов. Тем не менее разрешающая способность по времени оставляет желать лучшего – функция обновляет своё значение всего 66 раз за секунду, таким образом, средний шаг квантования составляет 15 мс. Рассмотрение значений функции также свидетельствует о шаге в 15 мс. Отсюда следует, что точно измерять длительности менее 15 мс при помощи данной функции невозможно. Дополнительная нагрузка на систему, создаваемая запущенным приложением, приводит к снижению частоты вызовов. Возвращаемые значения имеют прежний шаг квантования. Для устранения эффекта, создаваемого нагрузкой, следует задать приоритет реального времени процессу, регистрирующему работу CLK.
Остальные функции при дополнительной нагрузке будут вести себя аналогично.
Функция GTC позволяет выполнить в среднем столько же вызовов в секунду, сколько и CLK. Разрешающая способность – те же 15 мс. Таким образом, функции отличаются только единицами измерения: такты или миллисекунды.
Функция TGT в базовом варианте применения обладает тем же шагом квантования в 15 мс. Однако отличительной особенностью данной функции является её ориентация на использование в мультимедийных приложениях. Данный тип программного обеспечения выдвигает более жёсткие требования к быстродействию, поэтому API Windows предоставляет дополнительные функции для работы с таймером. Функция
timeBeginPeriod
timeGetDevCaps
Функция QPC имеет следующую особенность: корректность возвращаемых ею значений зависит от конфигурации используемой ПЭВМ. Общий смысл возникающего эффекта состоит в следующем. Поток приложения (даже однопоточного) может последовательно выполняться на разных ядрах процессора. По умолчанию Windows использует нежесткую привязку потоков к процессорам [18] в результате чего два последовательных вызова приложением функции могут быть выполнены на разных процессорах (ядрах). На некоторых многоядерных процессорах при работе в ОС Windows Server 2000, Windows Server 2003 и Windows XP это приводит к сложной ситуации, вызванной разной, отличной от номинальной, частотой работы ядер. Такая ситуация обусловлена применением технологий автоматического понижения (AMD Cool'n'Quiet и Intel SpeedStep) или повышения (AMD Turbo Core и Intel Turbo Boost) частоты работы ядер. Таким образом, функция QPC будет работать некорректно: рассчитанное время может изменяться нелинейно и даже идти вспять [9]. Данная ошибка признана разработчиком ОС, и может быть исправлена путем специального изменения настроек системы, которое описано в [8].
В ходе экспериментов, проведенных после дополнительной конфигурации операционной системы согласно [8], было установлено, что QPC может изменять своё состояние фактически каждую итерацию цикла без нагрузки, что для ПЭВМ, привлеченной к эксперименту, составляло 0,04 мс. Таким образом, после выполнения настроек [8], функция QPC обеспечивает разрешающую способность измерения времени, многократно превосходящую все другие функции.
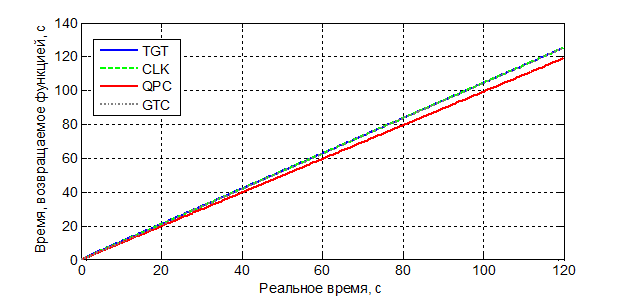
Рисунок 2 иллюстрирует показания рассмотренных функций от времени. Отметим, что при построении графика период изменения значений считался постоянным и равным величине, обратной средней частоте цикла без нагрузки, измеренной с помощью осциллографа.
Из графика видно, что наилучшие результаты даёт функция QPC, погрешность которой не превышает 0,04 мс на исследуемой ПЭВМ.
Методы стабилизации. Для обеспечения синхронизации при полунатурном моделировании разработчику системы в общем случае необходимо реализовать алгоритм, который в ходе работы выдаёт синхроимпульсы с заданной частотой. В силу ряда обстоятельств: перманентных и стохастических задержек, вызванных «тяжёлыми» частями программы и особенностями менеджмента ресурсов в Windows – частота опроса «тактового генератора» (то есть части алгоритма, отвечающей за выработку сигнала синхронизации) может падать, а сами запросы могут «не попадать» во временные узлы. Для компенсации ошибок, вызванных запаздыванием реакции на истечение интервала времени, в ОС Windows и в других ОС можно воспользоваться следующими методами стабилизации.
- Стабилизация длины интервала. Алгоритм нацелен на обеспечение минимального расхождения фактического времени между двумя импульсами и заданной длиной интервала (L-стабилизация).
- Стабилизация по узлам. Алгоритм обеспечивает наименьшее отклонение времени фактической реакции от требуемого, даже если для этого придется скорректировать длину интервала (Т-стабилизация).
- Стабилизация по количеству импульсов. В случае запаздывания, алгоритм начинает выдавать импульсы с максимально доступной частотой, пока не будет компенсировано число пропущенных импульсов (N-стабилизация).
Примеры, описывающие работу алгоритмов стабилизации, приведены ниже.
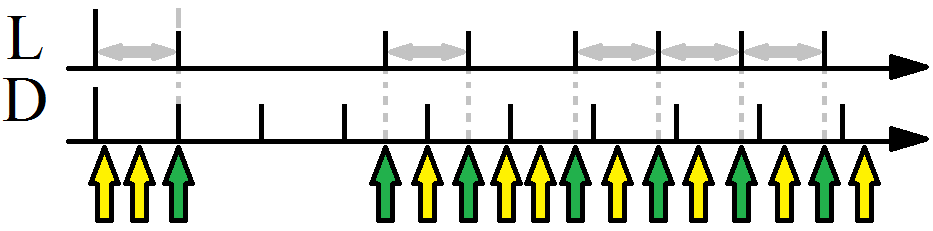
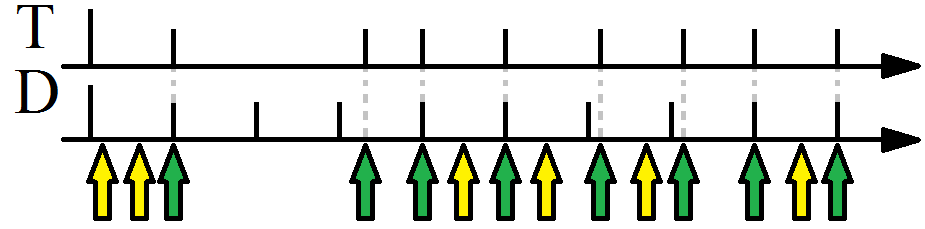
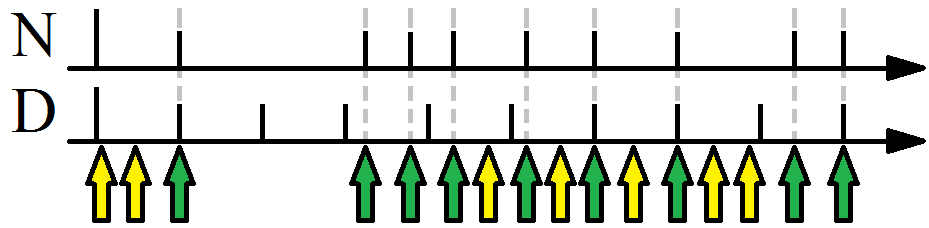
На рисунке 3 представлены две функции от времени. Первая из них принимает высокий уровень при кратности её аргумента dt:
где dt - длина отслеживаемого интервала времени.
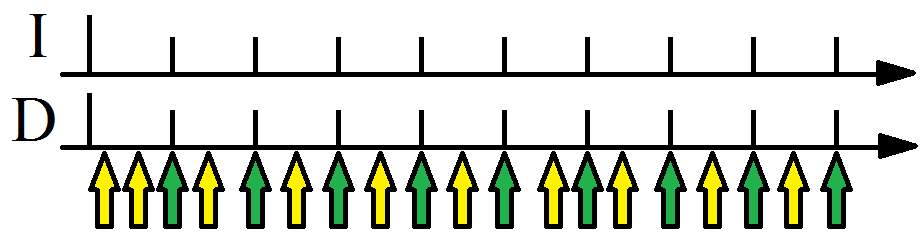
Стрелками на рисунке показаны запросы внешней части алгоритма, результата истечения периода времени. В идеальном случае частота запросов будет достаточной для наступления синхроимпульсов и соответствовать графику функции I(t). Запросы, приводящие к выдаче синхроимпульса, отмечены зелёным.
Метод стабилизации разрешает импульс, если разница между текущим временем (Tcur) и временем последнего (n-ого) импульса (Timpn) превышает или равна dt:
Tcur-Timpn⩾dt
После разрешения импульса, значение времени последнего импульса необходимо обновить:Timpn+1=Tcur
Используя разные алгоритмы вычисления значения Timpn+1, можно регулировать время наступления следующего импульса.На рисунке 4 представлен пример работы алгоритма стабилизации длины интервала (L-стабилизация). Интервалы, для которых удалось выдержать заданную длину, отмечены двунаправленной горизонтальной стрелкой. Нетрудно заметить, что алгоритм приводит к медленному дрейфу границ интервала вправо и, в конечном счёте, к потере некоторого количества интервалов. Последнее можно рассматривать как падение средней частоты следования импульсов. Кроме того, алгоритм не восприимчив к ошибкам, превышающим длину интервала: на приведенном рисунке пропуск второго и третьего интервалов воспринимаются как пропуск одного интервала. Одно из применений L-стабилизации: решение проблемы частых вызовов, при которых dt, в силу ограниченной разрешающей способности функции измерения времени, может часто принимать нулевые значения.
Для данного метода время наступления импульса:
Timpn+1=Tcur
На рисунке 5 представлен пример работы алгоритма стабилизации по временным узлам (T-стабилизация). Данный метод лишён отмеченного выше недостатка - дрейфа границ. Но за это приходится «платить» непостоянством величины интервала: именно изменяя его, алгоритм «притягивает» импульсы к нужным моментам времени. Метод, как и предыдущий, «игнорирует» ошибки, превышающие длину интервала. Время наступления импульса:
где int - целая часть действительного числа.
На рисунке 6 представлен пример работы алгоритма стабилизации по количеству импульсов (N-стабилизация). Преимущество метода – учёт больших ошибок (длиной более интервала). Недостаток – существенное искажение длин интервалов. Данный алгоритм время наступления импульса рассчитывает по формуле:
Timpn+1=Timpn+dt
В зависимости от поставленных целей при выполнении полунатурного моделирования в реальном масштабе времени необходимо выбрать один из рассмотренных методов.
Многопоточность. При моделировании задач пилотирования в реальном масштабе времени немалую часть итерации цикла моделирования занимают задачи визуализации рабочей области (внекабинной обстановки, показаний приборов) и опроса устройств ввода.
При реализации таких моделей преимущество имеют многопроцессорные системы [19, 20]. Процесс опроса устройств (в зависимости от времени одной его итерации) можно вынести в отдельный поток, реализовав его "конвейерную" обработку [9- 11].
Задачу визуализации также можно вынести в отдельный поток, одновременно снизив частоту обновления изображения (frames per second, FPS) до практически обоснованного значения (≈25Гц [12]). Выполняясь на другом ядре, визуализация не будет вносить дополнительных задержек в цикл моделирования.
Данное решение позволяет добиться значительного прироста точности синхронизации. Необходимым условием, очевидно, является наличие ПЭВМ с двумя и более процессорами (ядрами).
2 Сравнение методов синхронизации путем решения идентификационной задачи по данным стендового моделирования
В качестве обобщенного критерия сравнения различных вариантов синхронизации информационных потоков при полунатурном моделировании движения летательных аппаратов (ЛА) предлагается использовать одну из наиболее сложных задач обработки полетных данных - раздельную идентификацию сил тяги и сопротивления. В качестве меры точности синхронизации предлагается принять погрешности оценок, например, силы тяги, вычисленные по результатам моделирования на полунатурном стенде.
Рассмотрим краткую постановку задачи, детальное рассмотрение которой дано в [4-5].
Выпишем уравнение сил, действующих на ЛА вдоль связанной с самолетом продольной оси ОХ:
где Px(t) – проекция силы тяги; nx(t) – составляющая вектора перегрузки;
Cx(t) – коэффициент продольной аэродинамической силы;
q(t) – скоростной напор; m – масса самолета; S – площадь крыла.
Подставим в уравнение (1) результаты измерений, выполненных в полете, содержащие погрешности. В результате получим:
где ε(t) – погрешности измерений.
При практическом применении модели (2) целесообразно учесть, что аэродинамические коэффициенты силы сопротивления и подъемной силы лучше представлять в полусвязанной системе координат, где для углов атаки горизонтального полета имеют место формулы
где α - угол атаки, градус; δВ - отклонение руля высоты.
Соответственно при обработке следует использовать проекции вектора перегрузки на оси полусвязанной системы, которые выражаются через измеряемые на борту перегрузки в связанной системе координат по формулам, учитывающим угол атаки:
Необходимо также принять во внимание, что двигатели, как правило, устанавливаются так, что ось двигателя образует с продольной осью связанной системы координат угол установки двигателей φдв≠0. Кроме того, вектор силы тяги двигателя, строго говоря, представляет собой сумму вектора входного импульса Pвх, направленного по набегающему потоку, то есть вдоль полусвязанной оси, и вектора выходного импульса Pвых, направленного вдоль оси двигателя. Получим теперь окончательные выражения для проекций перегрузок на полусвязанные оси, используя разложения аэродинамических коэффициентов (3):
где εX, εY - погрешности измерения продольной и нормальной перегрузок.
Для оценивания тяги и сопротивления рекомендуется рассматривать первое уравнение, поскольку влияние выходного импульса во втором уравнении мало при углах атаки, близких к горизонтальному полету.
Анализ показывает, что для обеспечения идентифицируемости входной импульс Pвх следует принять согласно априорным данным. Тогда оценки коэффициентов силы сопротивления и выходного импульса Pвых можно найти стандартным методом наименьших квадратов (МНК) [13]. При этом вектор идентифицируемых параметров принимает вид:
Как известно [13], недостатком стандартного МНК является ухудшение точности оценок при наличии шумов измерения регрессоров, которыми в данном примере являются скоростной напор и угол атаки. Эффективным методом подавления шумов измерений является их фильтрация на основе численного интегрирования системы дифференциальных уравнений пространственного движения ЛА [14]. Описание алгоритма фильтрации дано в [15]. Прошедшие через фильтр данные далее обрабатываются тем же с алгоритмом МНК.
По отношению к точности синхронизации два указанных метода имеют следующие особенности. Для стандартного МНК требуется точное соответствие между выходным сигналом и регрессорами (в данном случае это продольная перегрузка, угол атаки и скоростной напор) только в дискретные моменты времени tk, k=1,2,...N При этом точность выдерживания интервала Δt=tk+1-tk значения не имеет, поскольку уравнение (4) является не дифференциальным, а алгебраическим.
Алгоритм фильтрации использует численное интегрирование дифференциальных уравнений движения ЛА, поэтому точность выдерживания интервала Δt очень важна.
В таблице 1 представлены относительные погрешности оценок силы тяги двигателя, полученные методом идентификации по результатам моделирования тестового полетного режима на полунатурном стенде в реальном масштабе времени.
Таблица 1 - Относительные погрешности идентификации силы тяги по данным стендового моделирования при различных способах синхронизации
Способ синхронизации |
Относительная погрешность, % | |||
| Измеренные данные без шума измерений | Фильтрованные данные без шума измерений | Измеренные данные с шумом измерений | Фильтрованные данные с шумом измерений | |
| 1 поток, T-стабилизация, заданная частота регистрации и визуализации | 0,035 | 0,319 | 0,4655 | 0,0345 |
| 1 поток, L-стабилизация, заданная частота регистрации и визуализации | 0,06 | 12,845 | 12,8448 | 0,0776 |
| 1 поток, L-стабилизация, с учетом снижения средней частоты регистрации и визуализации | 0,181 | 3,8362 | 0,2672 | 3,8879 |
| 1 поток, L-стабилизация, с учетом снижения средней частоты регистрации и с ограничением шага моделирования | 0,017 | 0,431 | 0,4914 | 0,0862 |
| 2 потока, заданная частота регистрации, без ограничения частоты визуализации (FPS) | 0,0086 | 0,0517 | 0,4741 | 0,2414 |
| 2 потока, заданная частота регистрации, с ограничением частоты визуализации (FPS), L-стабилизация | 0,0086 | 0,0517 | 0,4655 | 0,2155 |
| 2 потока, заданная частота регистрации, с ограничением частоты визуализации (FPS), T-стабилизация | 0,0129 | 0,0474 | 0,4647 | 0,2112 |
| 2 потока, заданная частота регистрации, с ограничением частоты визуализации (FPS), N-стабилизация | 0,0121 | 0,0517 | 0,4672 | 0,2112 |
В первых четырех строках таблицы приведены результаты для однопоточной организации моделирования, то есть без распараллеливания процессов вычислений и ввода-вывода. Из таблицы видно, что при однопоточной архитектуре выбор метода стабилизации и ограничений на частоту регистрации данных, частоту выдачи данных для визуализации, величину шага вычислений при моделировании уравнений движения ЛА существенно влияют на результат. Во втором и третьем столбцах таблицы показаны погрешности обработки данных без моделирования шумов измерений, вычисленные стандартным МНК непосредственно по измерениям и по измерениям, прошедшим фильтрацию. Очевидно, что для случая отсутствия шумов измерений фильтрация не требуется, потому что и стандартные оценки должны быть хорошими. Действительно, погрешности во втором столбце весьма малы и составляют сотые доли процента. Погрешности в третьем столбце значительно выше 0,3...12.8%. Это указывает на наличие погрешностей синхронизации, которые ухудшают оценки, вычисленные по фильтрованным данным. Анализ первых четырех строк показывает, что наилучшую синхронизацию при однопоточной архитектуре обеспечивают T-стабилизация и L-стабилизация с дополнительными настройками ( учет снижения частоты и ограничение шага вычислений при моделировании). В двух последних столбцах таблицы показаны погрешности оценок при добавлении шумов измерений. В этом случае, как и следовало ожидать, фильтрация улучшает результат.
В последних четырех строках таблицы 1 представлены результаты оценивания для различных вариантов двухпоточной архитектуры. Погрешности при отсутствии шумов весьма малы, как для непосредственно измеренных, так и для фильтрованных данных. Это указывает на высокую точность синхронизации при использовании распараллеливания потоков, которая практически не вносит погрешностей в операцию численного интегрирования. При наличии шумов измерений фильтрация также улучшает точность оценок ( столбцы четыре и пять).
Заключение
Выполненный анализ инструментов операционной системы Windows, предназначенных для синхронизации вычислений и ввода-вывода данных в реальном масштабе времени, а также решение тестовой идентификационной задачи показывают:
- Система Windows обеспечивает высокую точность синхронизации при полунатурном моделировании полета ЛА в реальном масштабе времени при разделении процесса моделирования на 2 потока ( решение уравнений моделирования и ввод-вывод данных), что требует ПЭВМ не менее чем с двумя процессорами.
В этом случае влияние погрешностей синхронизации на результаты моделирования полета пренебрежимо мало.
- Система Windows при однопоточной организации процесса моделирования обеспечивает удовлетворительную точность моделирования при использовании Т-стабилизации, а также при L-стабилизация с дополнительными настройками (учет снижения частоты и ограничение шага вычислений при моделировании).
- Для измерения времени следует применять функцию QPC с дополнительной настройкой параметров системы согласно [8].
- Эксперименты, представленные в данной работе, выполнялись для OC Windows 7 и Windows XP, однако выявленные закономерности с высокой вероятностью можно распространить на другие системы семейства Windows, поскольку используемые инструменты являются для них общими.
Работа выполнена при поддержке Российского фонда фундаментальных исследований (РФФИ), проект 12-08-00682-а.
Список литературы
- Кувшинов В.М., Анимица О.В. Программный комплекс FLIGHTSIM для моделирования и анализа динамики самолета с системой управления в среде MATLAB/SIMULINK // Труды конференции «Проектирование инженерных и научных приложений в среде MATLAB». – М.: ИПУ РАН. 2002. С. 638-650.
- Корсун О.Н., Бурлак Е.А., Набатчиков А.М. Исследовательский полунатурный стенд для анализа задач пилотирования и алгоритмов обработки полетных данных // Седьмой международный аэрокосмический конгресс IAC’2012. Сб. научн. тр. М.: 2013. 1 электрон. опт. диск (CD-ROM) рег. № 0321303652/03.06.2013.
- Таненбаум Э. Современные операционные системы. 3-е изд. – СПб.: Питер, 2010. 1120 с.
- Корсун О.Н., Поплавский Б.К., Леонов В.А. Оценивание силы тяги двигателей воздушных судов по данным летных испытаний на основе оптимальных инвариантных линейных преобразований // Техника воздушного флота. 2011. № 1. С. 25-30.
- Корсун О.Н., Леонов В.А., Поплавский Б.К. Оценивание силы тяги двигателей и аэродинамического сопротивления по данным летных испытаний // Седьмой международный аэрокосмический конгресс IAC’2012. Сб. научн. тр. – М.: 2013. 1 электрон. опт. диск (CD-ROM) гос. рег. № 0321303652/03.06.2013.
- Тихонов А.Н., Арсенин В.Я. Методы решения некорректных задач. – М.: Наука, 1988. 288 с.
- Почему не стоит разгонять таймер Windows или мегаватты, потраченные впустую // Хабрахабр. Блог компании Intel. Режим доступа: http://habrahabr.ru/company/intel/blog/186998/ (дата обращения 11.09.2013)
- Programs that use the QueryPerformanceCounter function may perform poorly in Windows Server 2000, in Windows Server 2003, and in Windows XP // Microsoft Technical support. Режим доступа: http://support.microsoft.com/kb/895980/en-us?fr=1 (дата обращения: 05.09.2013)
- Огинский А.А., Набатчиков А.М., Бурлак Е.А. Организация межпотокового взаимодействия с использованием объектов ядра операционной системы // Вестник компьютерных и информационных технологий. – 2012. №8. С. 52-56.
- Огинский А.А., Набатчиков А.М., Бурлак Е.А. Организация межпотокового взаимодействия с использованием объектов ядра операционной системы // Вестник компьютерных и информационных технологий. – 2012. №7. С. 48-52.
- Бурлак Е.А., Набатчиков А.М., Огинский А.А. Повышение производительности систем моделирования полёта на базе многоядерных ПЭВМ. // Сб. докл. IX-й Всерос. науч.-техн. конф. "Проблемы совершенствования робототехнических и интеллектуальных систем летательных аппаратов". - М.: МАИ-ПРИНТ, 2012. С. 334-339.
- Пескин А.Е., Труфанов В.Ф. Мировое вещательное телевидение. Стандарты и системы: Справочник. – М.: Горячая Линия – Телеком, 2004. 308 с.
- Корсун О.Н. Методы параметрической идентификации технических систем: Учебное пособие. МГТУ им. Н.Э. Баумана, Режим доступа: http://db.inforeg.ru/deposit/Catalog/mat.asp?id=286062, зарегистрировано во ФГУП "Информрегистр", № 0321100941, 2011.
- Корсун О.Н., Веселов Ю.Г., Гулевич С.П. Прогнозирование параметров движения самолета на основе идентификации упрощенной линейной модели // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2011. № 12. Режим доступа: http://technomag.bmstu.ru/doc/290540.html (дата обращения 25.09.2013).
- Корсун О.Н., Мотлич П.А. Комплексный контроль бортовых измерений основных параметров полета летательного аппарата // // Наука и образование. МГТУ им. Н.Э. Баумана. Электрон. журн. 2013. № 1. Режим доступа: http://technomag.edu.ru/doc/508634.html (дата обращения 25.09.2013).
- Страуструп Б. Язык программирования С++. – М.: Бином, 2011. – 1136 с.
- Осциллограф-мультиметр С1-112. Техническое описание и инструкция по эксплуатации ГВ2.044.124 ТО. 1984.
- Рихтер Дж. Windows для профессионалов: создание эффективных Win32 приложений с учетом специфики 64-разрядной версии Windows/Пер. c англ – 4-е изд. – Питер, Русская Редакция. 2001. – 752 с.
- Шилдт Г. Искусство программирования на С++, СПб.: БХВ-Петербург , 2005 г. – 496 с.
- Таненбаум Э. Архитектура компьютера. 5-е изд. – СПб.: Питер, 2007. – 844 с.: ил.
- Работа с LPT под Win 2000, XP: библиотека inpout32.dll // KERNELCHIP. Режим доступа: http://www.kernelchip.ru/pcports/PS002.php (дата обращения 15.10.2013).
- Про MinGW и LPT // Режим доступа: http://boorick.livejournal.com/30856.html (дата обращения 15.10.2013).
- Ан П. Сопряжение ПК с внешними устройствами: Пер. с англ. – М.: ДМК Пресс, 2001. – 320 с.: ил.

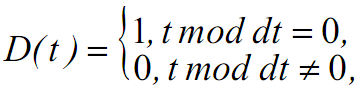

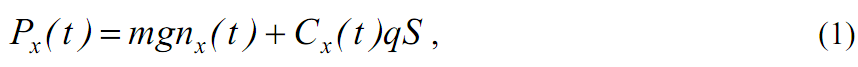
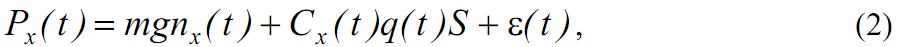
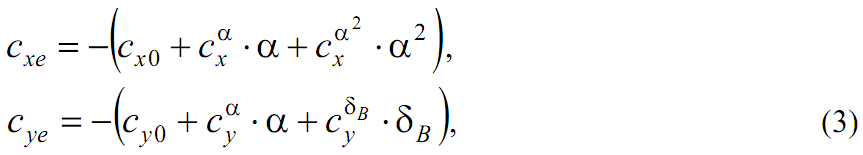
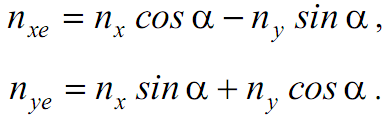
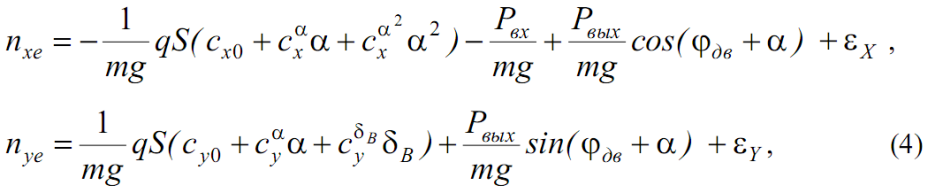
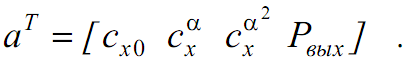
Комментарии