Задача про пятизначное число
Просмотров: 2856
25 февраля 2017 года
Постановка задачи
На неделе мне рассказали любопытную задачу. Отдалённо она напоминает задачки из ЕГЭ по информатике, но несколько сложнее.
Обозначим через S(k) сумму цифр числа k. Пусть n - наименьшее натуральное число такое, что S(n)+S(n+61)=4000. В ответ запишите пятизначное число, первые две цифры которого совпадают с первыми двумя цифрами числа n+61, а последние три - с последними тремя цифрами числа n+61. Например, если n+61=1234567890, то в ответ нужно записать число 12890.
Правильный ответ (его никто и не скрывает, так как суть - в решении):
59959
Негодование и демагогия
Нет, ну Вы видели:
... сумму цифр числа ...
Какая система счисления? Подозреваю, что позиционная - с каким основанием? Для задачки по математике - непозволительная небрежность в формулировках.
Какое, кстати, большое число получается: (4000/2)/9≈222 цифры. Неудивительно, что в ответ надо записать лишь его часть. Почему в ответ пойдут именно "голова" и "хвост"? - об этом ниже.
Решение
Рассмотрим число K, запись которого в десятичной позиционной системе счисления представляет собой последовательность цифр k1, k2, k3, ..., km:
K = {k1, k2, k3, ..., km} = k1*10m-1+k2*10m-2+...+km*10m-m.
Как это и бывает в задачах - многое сокрыто в мелочах: мы ищем наименьшее натуральное число. Нетрудно заметить, что при постоянном S(k), уменьшить число - значит переставить его цифры так, чтобы наименьшие шли при больших весах. Говоря иначе:
Например, Вас устраивает S числа 312, но хочется, чтобы число было меньше. Отсортируем цифры - получим число 123 с тем же значением S.
Вторая, ещё более очевидная мысль: натуральное число тем меньше, чем короче его запись в позиционной систем счисления. Отсюда следует, что получить искомую величину S нужно из числа, с наименьшим количеством цифр. А последнее, в свою очередь, говорит о том, что большая (в общем случае - не меньшая, если, конечно, S⩾9) часть цифр в этом числе - девятки.
Дополнительная мысль: сумма положительных чисел тем больше, чем больше каждое слагаемое. Таким образом, в нашей задаче надо стремится максимизировать и S(n), и S(n+61).
Рассмотрим число (n+61), а конкретно: как образуется его "хвост"
Помня о сказанном выше, рассмотрим: какие наилучшие значения могут быть у nm-2, nm-1, nm.
Для разряда nm, очевидно, лучшим значением будет 8:
8+1=9.
В этом случае, и nm, и n'm имеют максимальные значения, не противоречащие тождеству. (n'm=9.)
Перейдём к следующему разряду (рассмотрим возможные варианты):
| nm-1 | n'm-1 | S |
| 0 | 6 | 6 |
| 1 | 7 | 8 |
| 2 | 8 | 10 |
| 3 | 9 | 12 |
| 4 | 0 | 4 |
| 5 | 1 | 6 |
| 6 | 2 | 8 |
| 7 | 3 | 10 |
| 8 | 4 | 12 |
| 9 | 5 | 14 |
Наибольшему значению S соответствует nm-1=9; при этом n'm-1=5. Обратите внимание: так как 9+5=14>9, выражение для разряда nm-2 принимает следующий вид:
nm-2+1+0=n'm-2.
Ещё одно слагаемое - результат переноса из младшего разряда. Аналогично ситуации с разрядом nm, лучшим значением для nm-2 будет 8. (n'm-2=9.)
Исходя из произведённого анализа, исследуемые числа будут иметь вид:
- За исключением последних трёх цифр, числа n и (n+61) совпадают.
- Не считая последних трёх цифр, в числах присутствует не менее p девяток в каждом (они, будучи максимально сдвинуты вправо, образуют основную "массу" S, при сохранении минимальности n).
- Для обеспечения равенства S(n)+S(n+61)=const, в числах присутствует блок x, составленный из цифр, меньше 9. Для минимизации n, блок идёт в самом начале числа (до девяток). Так как остаток, не представимый в виде суммы девяток, не может превосходить или равняться девяти (иначе его можно записать как 9+y, что противоречит его определению), его запись занимает одну цифру.
S(n)+S(n+61)=4000
2*x+2*p*9+8+9+8+9+5+9=4000
2*x+18*p+48=4000
x+9*p+24=2000
x+9*p=1976.
2*x+2*p*9+8+9+8+9+5+9=4000
2*x+18*p+48=4000
x+9*p+24=2000
x+9*p=1976.
Находим p как floor(1976/9)=219 (ищем количество девяток, сумма которых приближается к 1976). Тогда:
x+9*219=1976
x=1976-1971
x=5.
x=1976-1971
x=5.
Итоговый вид чисел:
Ответ: "59"+"959"=59959.



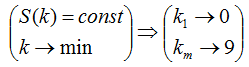
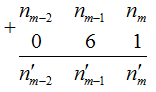
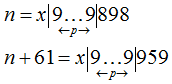
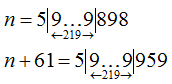
Комментарии