"К вопросу о разрезании пиццы" или "лайфхак вековой давности"
Просмотров: 1696
20 декабря 2016 года
Как декабрь, так я пишу про применение математических методов к бытовым манипуляциям с пиццей. Несколько лет назад я наткнулся в Интернете на материал (не помню: был он оформлен в виде слайдов или видео), рассказывающий, как на большой вечеринке по-тихому умыкнуть себе дополнительную порцию пиццы так, чтобы никто не заподозрил.
Руководство было адресовано хозяину вечеринки или лицу, ответственному за встречу курьера и подачу пиццы гостям. Хитрость крылась в сложности визуального различия круга и подобной ему фигуры, составленной из обрезанных сегментов исходного круга. К тому же, новая фигура подавалась уже разрезанной на подобие секторов.
Грамотная модификация фигуры позволяет не вносить заметных коррекций в форму пиццы, при этом уменьшить общую площадь подаваемого гостям блюда в пользу хитреца. Действовать надо по следующей схеме.
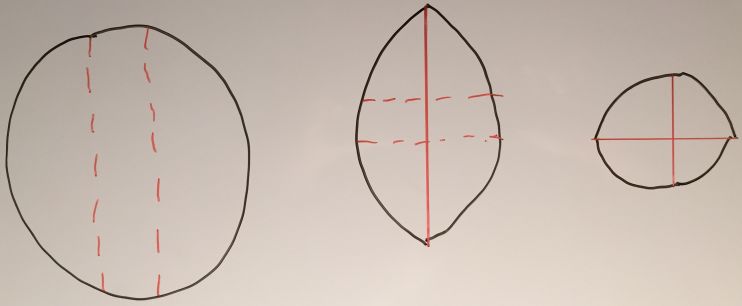
Сперва вырезается центральная часть (почти прямоугольник) и изымается, затем вырезается полоса, перпендикулярная только что изъятой. Оставшиеся четыре части сдвигаются и режутся на сектора как обычно. Изъятое съедается или откладывается до лучших времён.
При должной сноровке, радиус новой пиццы будет визуально неотличим от исходной. Да и гости просто не будут ожидать такого коварства! В общем - свежее молодёжное решение. Но есть одно, но.
Двадцатого декабря 1906 года (110 лет назад!), в журнале Nature, была опубликована маленькая заметка под заголовком "Cutting a Round Cake on Scientific Principles". Работа (в разделе "Letters to the editor") подписана как "F.G." (я встречал мнение, что авторство принадлежит сэру Фрэнсису Гальтону). Ниже я приведу ссылку на данную публикацию в архиве журнала, чтобы Вы смогли ознакомиться с работой на языке оригинала (по умолчанию доступна только аннотация, но в неё помещается весь текст заметки кроме рисунка).
В работе автор приводит решение следующей проблемы: минимизация площади поверхности, подвергающейся заветриванию в процессе хранения частично съеденного торта. Как можно догадаться, алгоритм соответствует рассмотренному ранее (но допускает итерации).
Вот так: всё новое - это хорошо забытое старое.
Руководство было адресовано хозяину вечеринки или лицу, ответственному за встречу курьера и подачу пиццы гостям. Хитрость крылась в сложности визуального различия круга и подобной ему фигуры, составленной из обрезанных сегментов исходного круга. К тому же, новая фигура подавалась уже разрезанной на подобие секторов.
Грамотная модификация фигуры позволяет не вносить заметных коррекций в форму пиццы, при этом уменьшить общую площадь подаваемого гостям блюда в пользу хитреца. Действовать надо по следующей схеме.
Сперва вырезается центральная часть (почти прямоугольник) и изымается, затем вырезается полоса, перпендикулярная только что изъятой. Оставшиеся четыре части сдвигаются и режутся на сектора как обычно. Изъятое съедается или откладывается до лучших времён.
При должной сноровке, радиус новой пиццы будет визуально неотличим от исходной. Да и гости просто не будут ожидать такого коварства! В общем - свежее молодёжное решение. Но есть одно, но.
Двадцатого декабря 1906 года (110 лет назад!), в журнале Nature, была опубликована маленькая заметка под заголовком "Cutting a Round Cake on Scientific Principles". Работа (в разделе "Letters to the editor") подписана как "F.G." (я встречал мнение, что авторство принадлежит сэру Фрэнсису Гальтону). Ниже я приведу ссылку на данную публикацию в архиве журнала, чтобы Вы смогли ознакомиться с работой на языке оригинала (по умолчанию доступна только аннотация, но в неё помещается весь текст заметки кроме рисунка).
В работе автор приводит решение следующей проблемы: минимизация площади поверхности, подвергающейся заветриванию в процессе хранения частично съеденного торта. Как можно догадаться, алгоритм соответствует рассмотренному ранее (но допускает итерации).
Вот так: всё новое - это хорошо забытое старое.

Комментарии