Коварные невидимые горизонтали
Просмотров: 6571
03 января 2017 года
Постановка задачи
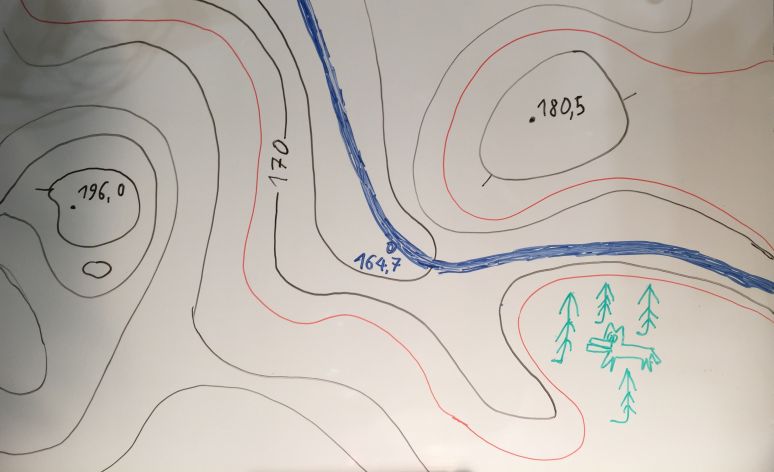
Принесли мне недавно посмотреть актуальные задания по географии для 5-ого класса. Так как на оригинальной карте уже был выполнен ряд построений, то здесь привожу свою "кавер-версию" оной:
Итак, парочка заданий:
2. Определите, через сколько метров проведены горизонтали на плане местности.
…
5. Выделите коричневым (у меня только красный маркер - не обессудьте) цветом утолщённую горизонталь, соединяющую точки с абсолютной высотой 175 м. Через сколько метров проведены утолщённые горизонтали, если на плане показана только одна из них - 175 м. Предложите свои варианты ответа.
Комментарий к решению
Никогда особо не увлекался географией, поэтому подошёл к решению с формальной стороны. Я предлагаю алгоритм решения, который любителям географии может показаться странным и отрешённым от сути проблемы.
Вопрос №2 - формальное решение
Ну, тут всё просто: находим известную горизонталь (тут подписана только одна - 170 м.) - обозначим её высоту как H, находим ещё одну отметку, желательно, с максимально удалённой по модулю величиной. Из известных высот остаются 196 м., 164,7 м. и 180,5 м. Точка с наибольшим перепадом высот, относительно 170 м. - 196 м., обозначим её высоту как P.
Теперь надо посчитать количество горизонталей (N) между двумя выбранными точками. Необходимо учесть, что в процессе движения от первой точки ко второй, одна и та же высота может повторяться. Для правильного подсчёта, необходимо выбрать ближайшую к точке P точку на горизонтали H. (Или не считать повторяющиеся горизонтали: здесь аналогия с открывающимися/закрывающимися скобками и уровнем вложенности.)
Например, если двигаться к точке 180,5 из точки A (см. рисунок), то N=5, а если из точки B (и это правильно), то - 2.
Двигаясь из точки A к отметке 196 м., мы пересечём N=5 горизонталей.
Искомая величина Δ, удовлетворяет системе неравенств:
Δ<|H-P|/N,
Δ>|H-P|/(N+1).
Δ>|H-P|/(N+1).
Эту систему я собрал из двух простых условий: расстояние между горизонталями должно быть таким, чтобы одноврменно
- его хватало на N горизонталей;
- его не хватало на (N+1) горизонталь.
В нашем случае: H=170, P=196, N=5 - таким образом:
Δ<|170-196|/5,
Δ>|170-196|/(5+1).
Δ>|170-196|/(5+1).
Вычислим:
|170-196|/5=|-26|/5=26/5=5,2;
|170-196|/(5+1)=26/6=4,(3).
|170-196|/(5+1)=26/6=4,(3).
Логично предположив, что ответ должен быть целым, найдём решение системы:
Δ<5,2,
Δ>4,(3).
Δ>4,(3).
Ответ: Δ=5 м.
Мы могли выбрать и любую другую высоту в качестве точки P, например, 164,7 м. В этом случае:
Δ<5,3,
Δ>2,65.
Δ>2,65.
Этой системе, помимо найденного Δ=5, удовлетворяет и Δ=3 и Δ=4.
Вопрос №2 - решение для внимательных
Если прежде чем отвечать на второй вопрос, прочитать все предложенные задания, то из пятого можно узнать, что утолщённая горизонталь соединяет точки с высотой 175 м. Так как соседняя горизонталь подписана (170 м.), то:
Δ=175-170=5 м.
Вопрос №5
Через сколько метров проведены утолщённые горизонтали, если на плане показана только одна из них
Не знаю как Вас, а меня этот вопрос поразил формулировкой: на плане, мол, есть ещё особые горизонтали, но я Вам их не покажу - сами угадайте. Какого цвета невидимая линия? И, кстати, если это вопрос - почему в конце предложения нет вопросительного знака? Ах, да - мы же не на "русском".
Я, конечно, не блещу соображалкой, поэтому потребовалось перечитать вопрос несколько раз, пока, наконец, он не развернулся в понимании в следующую формулировку:
Характер рельефа (диапазон высот) фрагмента местности, отображённого на плане, таков, что содержит только одну особую горизонталь. Исходя из этого, определите: с каким шагом по высоте проведены особые горизонтали (которые, возможно, присутствуют на большем фрагменте плана)?
Рассуждая таким образом, можно заключить, что максимальный перепад высот относительно утолщённой горизонтали (175 м.) меньше искомого шага ΔB.
Проанализировав план, приходим к выводу:
ΔB>196-175,
ΔB>175-164,7.
ΔB>175-164,7.
Вычислим:
ΔB>21,
ΔB>10,3.
ΔB>10,3.
Второе условие избыточно, таким образом:
ΔB>21.
Анализируя план ранее, мы пришли к выводу, что расстояние между горизонталями (некоторые из которых утолщённые) - Δ=5 м. Значит, ΔB делится на 5 без остатка (иначе не попадёт в сетку).
Известная нам утолщённая горизонталь должна удовлетворять искомой ΔB, то есть 175 должно делиться на ΔB без остатка.
Резюмируя:
- ΔB>21;
- ΔB/5 - целое;
- 175/ΔB - целое.
Алгоритм следующий: найдём минимальное ΔB из условий (1) и (2), полученную оценку подставим в условие (3), получив максимальный делитель для последующего перебора (если x минимален, то y=const/x - максимален).
- ΔB>21;
- ΔB/5 - целое;
Находим минимальное ΔBmin, как (
ceil
ΔBmin=ceil(21/5)*5=ceil(4,2)*5=5*5=25.
Так как 175/ΔBmin=7, то осталось проверить числа 6, 5, 4, … Приступим к перебору.
| I | ΔB=175/I |
| 7 | 25 |
| 6 | дробное |
| 5 | 35 |
| 4 | дробное |
| 3 | дробное |
| 2 | дробное |
| 1 | 175 |
Таким образом, получаем три возможных ΔB:
ΔB1=25, ΔB2=35, ΔB3=175 -
но нас и предупреждали: "Предложите свои варианты ответа".
Если уж выбирать единственный ответ, то число должно быть удобным в использовании в качестве шага по высоте. Думается адекватным, сформулировать в качестве критерия "эргономичности числа" следующее выражение:
n=lg(ΔB*k),
где
lg
| k | n для ΔB1 | n для ΔB2 | n для ΔB3 |
| 1 | дробное | дробное | дробное |
| 2 | дробное | дробное | дробное |
| 3 | дробное | дробное | дробное |
| 4 | 2 | дробное | дробное |
Таким образом,
Ответ: ΔB=ΔB1=25 м.

Комментарии