Прорыв точности
Просмотров: 1013
25 января 2021 года
Вам, вероятно, приходилось сталкиваться с ожидаемыми ограничениями точности формата float. Уже привычно: проводить тест не на равенство переменных, а на предельную близость (модуль разницы не превосходит eps). Но, вероятно, сохраняя инерцию восприятия кодирования целых чисел в двоичной системе счисления, многие забывают о принципиальной невозможности хранить произвольные числа без оговорки о точности представления. Неудачно выбранная стратегия обработки значений float-переменных может обернуться сложно обнаруживаемыми багами.
Например, Python (примеры выполнялись on-line на сайте www.onlinegdb.com):
внезапно не радует результатом:
В Си, тем временем, всё замечательно. Но только на первый взгляд. Причина всему - IEEE 754. Казалось бы: уже были фокусы с NaN, досадные проблемы с type cast в Blitz, раздражающее исчерпание точности позиционирования полигонов 3D-модели при удалении от нуля - но, опять наступаю на старые грабли.
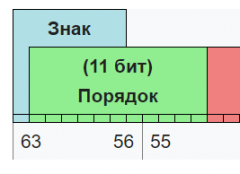
Руководствуясь этой схемой (и статьёй), легко и быстро можно написать функцию для "препарирования" float64 (double) на Си:
Как видно из кода, вместо нечитабельных предрассчитанных констант, в масках я использовал интуитивные вычисления типа, очевидно раскрывающие семантику манипуляций. Я не хотел использовать "магические" константы 8 и 8, обладающие разным смыслом ("количество бит в байте актуальных моделей ЭВМ" и "количество байт в float64-переменной", соответственно), но и загромождать код множеством производных констант - так же не хотелось. В результате - получилось как обычно: ни рыба, ни мясо, ни кафтан, ни ряса.
Как и в случае с изучением функций работы со временем, невозможно оценить эффекты функционирования инструмента, используя для измерений сам инструмент (хорошо, что в этот раз не надо собирать стенд из ПК и осциллографа). Тем не менее, ряд вычислений необходимо выполнить в сторонней системе (не использующей стандарт IEEE 754), например - в штатном калькуляторе Windows или СЧИТАЛЕ.
Итак, результаты запуска:
Проделав (надеюсь, нигде не ошибся) предложенные вычисления, получаем:
Этот результат согласуется с полученным на Python - вопрос лишь в форме представления (точности округления при операциях).
Например, Python (примеры выполнялись on-line на сайте www.onlinegdb.com):
Целое число умножается на не бесконечную дробь - что может пойти не так?
1 | print (6 * 0.15)
|
Гром среди ясного неба
1 | 0.8999999999999999
|
В Си, тем временем, всё замечательно. Но только на первый взгляд. Причина всему - IEEE 754. Казалось бы: уже были фокусы с NaN, досадные проблемы с type cast в Blitz, раздражающее исчерпание точности позиционирования полигонов 3D-модели при удалении от нуля - но, опять наступаю на старые грабли.
Руководствуясь этой схемой (и статьёй), легко и быстро можно написать функцию для "препарирования" float64 (double) на Си:
Препарирование double
123456789101112131415161718192021222324252627282930313233343536373839404142434445464748495051 | #include <math.h> #include <iostream> using namespace std; void double_struct_view(double x) { const unsigned char BYTE_SIZE = 8; // bit const unsigned char DOUBLE_SIZE = 8; // byte; sizeof(double) const unsigned long long DIV = pow(2, 52); cout << x << endl; unsigned char* txt = (unsigned char*)(&x); cout << hex; for (int i = DOUBLE_SIZE - 1; i >= 0 ; i--) cout << int(txt[i]) << '\t'; cout << endl; bool sgn = txt[DOUBLE_SIZE - 1] & (1 << (BYTE_SIZE - 1)); cout << "sgn = " << (sgn == 0 ? "pos" : "neg") << endl; unsigned char hb = int( txt[DOUBLE_SIZE - 1] & (~(1 << (BYTE_SIZE - 1))) ); unsigned char lb = int( txt[DOUBLE_SIZE - 2] & (~((1 << 4) - 1)) ) >> 4; int order = hb * (1 << 4) + lb; cout << dec << "order = " << order << endl; int m = int( txt[DOUBLE_SIZE - 2] & ((1 << 4) - 1) ); cout << hex << m << '\t'; for (int i = DOUBLE_SIZE - 3; i >= 0 ; i--) cout << int(txt[i]) << '\t'; cout << endl; unsigned long long p = 1; cout << dec << "X = "; for (int i = 0; i < DOUBLE_SIZE - 2; i++) { cout << (txt[i] * p) << " + "; p *= 256; } cout << (m * p) << ";" << endl; cout << "(1 + X / " << DIV << ") * " << pow(2, order - 1023) << endl; } int main() { double x = 6 * 0.15; double_struct_view(x); return 0; } |
Как видно из кода, вместо нечитабельных предрассчитанных констант, в масках я использовал интуитивные вычисления типа
(~((1 << 4) - 1))
Как и в случае с изучением функций работы со временем, невозможно оценить эффекты функционирования инструмента, используя для измерений сам инструмент (хорошо, что в этот раз не надо собирать стенд из ПК и осциллографа). Тем не менее, ряд вычислений необходимо выполнить в сторонней системе (не использующей стандарт IEEE 754), например - в штатном калькуляторе Windows или СЧИТАЛЕ.
Итак, результаты запуска:
Проделав (надеюсь, нигде не ошибся) предложенные вычисления, получаем:
0,89999999999999991118215802998748
Этот результат согласуется с полученным на Python - вопрос лишь в форме представления (точности округления при операциях).
Рекомендации
- Для межсистемной синхронизации использовать сырое представление чисел (дамп памяти), а не какие-либо высокоуровневые интерпретации.
- Всегда помнить об ограниченной точности: использовать округление с заданной грубостью, исходя из семантики кодируемых данных и потенциальных уязвимостей алгоритма (например, как мы рассмотрели в данной заметке, получение значений, кратных 0.15, при помощи формулы , обречено на потерю уровня 0.9).
i * 0.15


Комментарии