Волшебная дюжина
Просмотров: 1769
19 февраля 2017 года
Обновление: 24 февраля 2017
В манускриптах, тайны древних,
Как всегда, мистики полны,
Объяснений достоверных
Здравые требуют умы.
В заметке "Дедовский" способ генерации стандартного шума из равномерного я упомянул формулу дисперсии равномерного распределения:
Именно из этой формулы, в алгоритм генерации попадает одно из "магических чисел" (то есть, по выражению Стефана К. Дьюхэрста, число без внятной семантики, могущее означать всё что угодно). Тогда я не стал подробно останавливаться на этом, но два обстоятельства подтолкнули меня рассмотреть эту формулу детальнее:
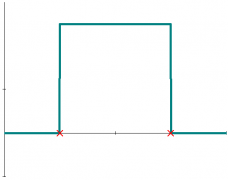
Непрерывное равномерное распределение на отрезке [a;b] обладает следующей функцией плотности вероятности f(x):
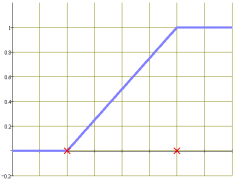
Соответственно, функция распределения F(x) имеет вид:
(F(x), впрочем, для вывода искомых формул не нужна.)
По определению, формулы математического ожидания и дисперсии н.с.в. [?]
Подставив в формулу м.о. [?]
Теперь вычислим дисперсию.
Нам необходимо будет взять кое-какой интеграл, для чего воспользуемся свойством
тогда интеграл:
Возвращаемся к дисперсии (аналогично случаю с M[X], рассмотрим три интервала, два из которых - априори нулевые):
воспользовавшись свойством формулы сокращённого умножения многочленов, получим:
Вот и образовалась дюжина.
В манускриптах, тайны древних,
Как всегда, мистики полны,
Объяснений достоверных
Здравые требуют умы.
- гр. Король и Шут «Ричард Гордон».
В заметке "Дедовский" способ генерации стандартного шума из равномерного я упомянул формулу дисперсии равномерного распределения:
(b-a)2/12.
Именно из этой формулы, в алгоритм генерации попадает одно из "магических чисел" (то есть, по выражению Стефана К. Дьюхэрста, число без внятной семантики, могущее означать всё что угодно). Тогда я не стал подробно останавливаться на этом, но два обстоятельства подтолкнули меня рассмотреть эту формулу детальнее:
- Желание полностью разобрать алгоритм генерации.
- Желание вспомнить: как вообще выводятся подобные формулы (мат. ожидания, дисперсии, проч.)?
Непрерывное равномерное распределение на отрезке [a;b] обладает следующей функцией плотности вероятности f(x):
Соответственно, функция распределения F(x) имеет вид:
(F(x), впрочем, для вывода искомых формул не нужна.)
По определению, формулы математического ожидания и дисперсии н.с.в. [?]
непрерывная случайная величина
выражаются через f(x), как:Подставив в формулу м.о. [?]
математическое ожидание
конкретную функцию плотности вероятности, получим:Теперь вычислим дисперсию.
Нам необходимо будет взять кое-какой интеграл, для чего воспользуемся свойством
тогда интеграл:
Возвращаемся к дисперсии (аналогично случаю с M[X], рассмотрим три интервала, два из которых - априори нулевые):
воспользовавшись свойством формулы сокращённого умножения многочленов, получим:
Вот и образовалась дюжина.

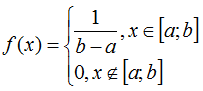
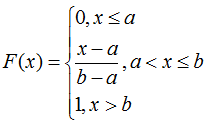
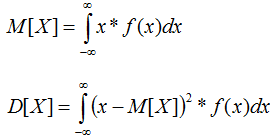
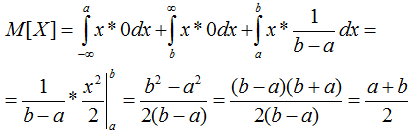
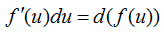
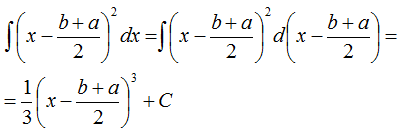
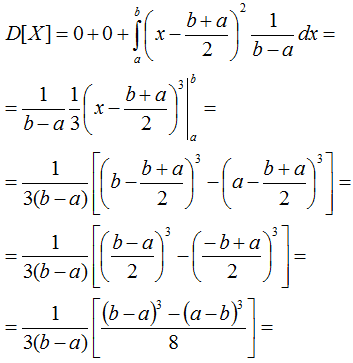
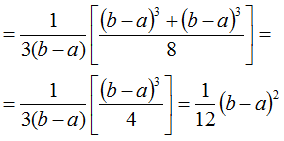
Комментарии