"Дедовский" способ генерации стандартного шума из равномерного

Просмотров: 7374
28 декабря 2015 года

Всякий, кто питает слабость к арифметическим методам получения случайных чисел, грешен вне всяких сомнений.

При моделировании различных возмущений и шумов реального мира, Вы рано или поздно сталкиваетесь с необходимостью программно генерировать шум, значения амплитуд которого распределены нормально:

Нормальное распределение, также называемое распределением Гаусса — распределение вероятностей, которое в одномерном случае задаётся функцией плотности вероятности, совпадающей с функцией Гаусса.

- Нормальное распределение

Ну а конкретнее: почти всегда выбирается так называемое "стандартное нормальное распределение":

Стандартным нормальным распределением называется нормальное распределение с математическим ожиданием μ = 0 и стандартным отклонением [?]

В отечественной литературе принято использовать термин "среднеквадратическое отклонение"

σ = 1.

- Нормальное распределение

Почему выбирается именно нормальное распределение? Большинство наблюдаемых в реальном мире шумов - сумма множества независимых случайных величин. По сути, в таком случае под шумом мы подразумеваем некий сигнал, объединяющий различные возмущения. (Этот эффект мы уже рассматривали - см. ссылки в конце.) Детализация слагаемых может быть недоступна или просто не иметь смысла в рамках задачи. Согласно центральной предельной теореме (Ц. П. Т.):

Сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.

- Центральная предельная теорема

Итак, необходимо получить стандартный шум. Обнаруживается следующая проблема: большинство языков имеет лишь один штатный ГПСЧ [?]

генератор псевдослучайных чисел

, обладающий равномерным распределением (и, часто, диапазоном возвращаемых значений от 0 до 1).

Самый простой метод генерации заключается в решении проблемы "в лоб". Необходимо просто сложить несколько случайных чисел - при достаточном количестве слагаемых мы будем получать величины, распределённые нормально. Этот факт вытекает из упомянутой выше Ц. П. Т.

Если бы в МАТЛАБ-е не было штатного генератора

randn

, то рассмотренный алгоритм можно было бы реализовать следующим образом:

Решение для MATLAB
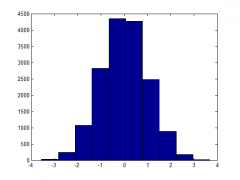
123456function [X]=MyRandn(L)
    X=zeros(1,L);
    for i=1:L
        X(i)=sum(rand(1,12))-6;
    end
end

Здесь функция

MyRandn

возвращает в точку вызова вектор из

чисел, значения которых распределены стандартно. Напомню, что функция

rand

возвращает числа от 0 до 1 включительно.

У внимательного читателя могут возникнуть три вопроса:

Почему из конечного результата вычитается 6?
Почему для суммирования берётся именно 12 чисел, а не, скажем, 100?
Почему в коде присутствуют так называемые "магические числа": величины, представленные литералами, а не именованными константами.

Число 6 вычитается для того, чтобы выход генератора соответствовал отрезку не [0; 12], а [-6; 6]. Иными словами, если бы мы взяли 100 слагаемых, то вычитали бы 100/2=50. Центровка необходима для обеспечения нулевого математического ожидания порождаемой последовательности.

Но почему 12 слагаемых? Здесь применяется некая оптимизация, времён тщательной экономии процессорного времени: именно сумма 12 чисел позволяет избежать использования (умножения) дополнительного нормировочного коэффициента.

При суммировании случайных распределений, особым образом суммируются и дисперсии распределений:

D[X+Y]=D[X]+D[Y]+2*cov(X,Y)

Так как величины независимы (исходный генератор порождает квазибелый шум), то ковариация (корреляционный момент) будет равняться нулю. Таким образом, сумма N случайных распределений (каждое с одинаковой дисперсией DD) будет обладать дисперсией (N*DD).

Согласно определению, нам необходимо добиться единичного среднеквадратического отклонения получаемой последовательности. А чему равна дисперсия равномерного распределения?

(b-a)²/12

В нашем ( [0; 1] ) случае - это 1/12. Нетрудно заметить, что если просуммировать именно 12 равномерных распределений, то мы получим единичную результирующую дисперсию, а, соответственно, и среднеквадратическое отклонение.

Таким образом, константы 12 и 6 не подразумевают изменения в ходе дальнейшей эксплуатации алгоритма без его дополнительной переделки.

Некоторые читатели пеняют мне на то, что я мало внимания уделяю Си\Си++ - пожалуйста:

Решение на языке C\C++
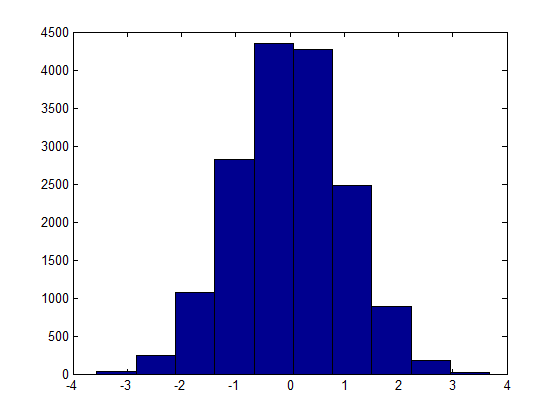
123456double normrand(){
    double x=0;
    for(short i=0;i<12;i++)
        x+=(rand()%1001)*0.001;
    return x-6;
}

Функция

normrand

возвращает одно случайное число. Если сгенерировать множество чисел, используя эту функцию, то можно показать, что их значения будут распределены стандартно.

При реализации на Си\Си++ обнаруживаем ещё одну проблему: штатный ГПСЧ генерирует целые числа [0;

RAND_MAX

]. Мне было лень привязываться к потенциально непереносимым решениям, и я поступил иначе.

Будем считать, что точности в 3 цифры после запятой нам достаточно. Тогда можно просто взять остаток от деления на 1001 и получить число из диапазона [0; 1000]. Теперь просто выполним десятичный сдвиг на 3 путём умножения на 10^-3 - получим [0; 1.000] - Voila!

Гистограмма последовательности, полученной от MyRandn

Отмечу, что для генерации стандартной нормально распределённой случайной величины прогрессивное человечество использует преобразование Бокса — Мюллера. Алгоритм не такой красивый (как прямая эксплуатация Ц. П. Т.), но позволяет получить из двух (а не 2*12=24) равномерных распределений два стандартных. Правда, в ходе вычисления используются трансцендентные функции, что может быть неудобно при реализации на некоторых языках и медленно для специфических вычислителей.

Запись опубликована в категориях:

Алгоритмы и аспекты

"Дедовский" способ генерации стандартного шума из равномерного

Внешние источники:

Комментарии