Создаём управляющую программу для своего портативного генератора равномерного дискретного белого шума
Просмотров: 2920
15 декабря 2015 года
Небольшой опрос показал, что большинство людей не видит необходимости иметь на инженерном калькуляторе клавишу генерации квазислучайного числа. Действительно, окружающий мир полон случайностей (их подлинную детерминированность или стохастичность оставим на откуп философам): от чего бы не взять в руки монетку или игральную кость? Но что делать, когда необходимо большее число состояний, чем может породить выбранный генератор? Большинство людей довольно быстро придумывает неправильное решение и довольствуется им.
Иными словами, получаемые с генератора значения должны быть равновероятны (то есть иметь равномерное распределение) и не зависеть от предшествующих состояний генератора (шум должен быть белым, то есть его автокорреляционная функция должна иметь вид δ-функции Дирака). Ну и - исходя из физической природы случайности (игральной кости), на которой работает наш более сложный генератор - выходная величина должна изменяться дискретно (никаких "2,5" и тому подобного).
Дискретность значений и необходимый вид функции автокорреляции гарантирует природа игральной кости. (Впрочем, это несложно испортить неудачным алгоритмом использования кубика.) Осталось разобраться с равномерностью распределения значений.
Игральные кости (с фотографии) уже убраны в коробку: для серьёзной работы такой инструмент не годится.
Для тестирования алгоритма генерации я буду использовать полюбившийся мне за годы эксплуатации метод математического моделирования. Эксперимент заключается в многократном повторении моделирования эпизода работы генератора. При достаточно большом количестве итераций, экспериментальный результат будет соответствовать аналитическому. Тем самым будет подтверждена корректность теоретических выкладок. Построить эксперимент подобным образом для данного типа задач, можно опираясь на Закон больших чисел:
Подробнее о методе Монте-Карло смотри здесь.
Необходимое количество итераций прикинем "на глаз", опираясь на динамику результатов и аналитику.
Опишем программную реализацию кубика с шестью гранями. Попутно будем считать количество вызовов (бросков кости), чтобы оценить сложность алгоритма.
Используемая здесь функция - встроенная в язык функция генерации псевдослучайного числа. Базируется, вероятнее всего, на линейном конгруэнтном генераторе. Последний имеет свои недостатки, которые нас не интересуют, так как реальная игральная кость ими не обладает. Впрочем, покажем корректность работы простого генератора в рамках тестового запуска.
Определим нулевой вариант решения, реализация которого нужна для тестирования работы установки.
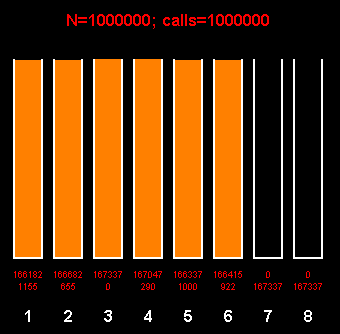
Представленный алгоритм порождает равномерное дискретное распределение чисел на отрезке [1;6].
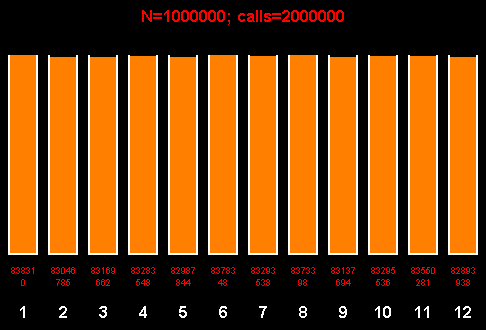
Как видно из рисунка, для генерации миллиона значений потребовался миллион бросков. Каждое число выпадало примерно одинаковое количество раз (3-яя снизу строка). Повторяя эксперимент, можно получить превалирование то одного, то другого исхода.
Как правило, это решение приводят первым. Сводится оно к тому, что кубик бросается несколько раз, при этом количество выпавших очков суммируется. Число бросков заранее оговаривается: его выбирают таким, чтобы максимальная сумма (с учётом коррекции) выпавших очков была не меньше правой границы генератора. Так как при помощи игральной кости нельзя выбросить "ноль очков", то сумма корректируется (с учётом левой границы генератора) соответствующим уменьшением. Если подобрать число бросков идеально не получается, и результирующая сумма превосходит максимальное выходное значение генератора, то от суммы берётся остаток от деления.
В нашем случае, для генерации понадобится два броска кубика (сумма может принимать значения от 2 до 12 включительно). Затем будет произведено вычитание двойки - сумма сдвинется до [0; 10]. Далее взятие остатка от деления - [0; 7]. И финальная коррекция - [1; 8].
Это ужасный алгоритм! Первое, на что стоит обратить внимание: это использование операции взятия остатка от деления. В случае, если мы берём остаток от деления на число, которое не кратно максимальному значению делимому числа, то мы получим "перекос" в распределении.
Действительно: числа 0, 1, 2, 3, 4, 5, 6, 7 - остаются на "своих местах", а числа 8, 9, 10 - преобразуются соответственно в 0, 1, 2. Вероятность выпадения первых трёх чисел возрастает.
Но это ещё не всё. Центральная предельная теорема говорит о том, что:
Все условия для наблюдения эффекта соблюдены.
Действительно: мы пытаемся свести 6×6=36 внутренних состояний генератора к 8-ми выходным значениям. Для сохранения равномерного распределения необходимо, чтобы каждое значение из [1; 8] можно было получить одинаковым количеством способов, а именно: 36/8=4,5. Уже нецелое число в ответе должно насторожить, но, чтобы окончательно убедиться в перекосах: минимальное число можно получить единственным способом. Последнее, правда, несколько компенсируется другим негативным эффектом (остатком от деления).
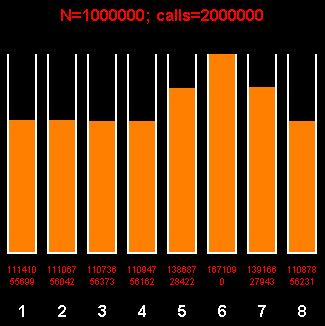
Суперпозиция эффектов порождает интересное распределение.
Основной негативный эффект (по-большому счёту, затмевающий перекос из-за использования остатка от деления) создаёт стремление получающегося распределения к распределениею Гаусса (как и ожидалось, исходя из Ц. П. Т.).
Для генерации понадобилось 2 миллиона бросков.
Заменив обычное суммирование взвешенной суммой, мы уйдём от условий, благоприятных для образования нормального распределения. В качестве взвешенной суммы, будем интерпретировать каждый бросок как цифру в некоей позиционной системе счисления. Очевидно, в данном случае, логично выбрать основание 6.
К аналогичному решению проще прийти из комбинаторных соображений.
Тем не менее, операция взятия остатка от деления осталась. Алгоритм плох! Так как 36/8=4,5, то можно предположить, что будет увеличена вероятность для 36-8*4=4-ых первых исходов, а отношение величин будет приблизительно (4+1)/4=5/4.
Предсказанное сбылось:
5/4=1,25
139446/111128≈1,25482...
Нетрудно заметить, что искомое число комбинаций представимо в виде произведения 8=2×2×2. (Здесь уместна аналогия: случайно выбираем половину интервала, затем делим её на две части и снова делаем случайный выбор и так далее.) Таким образом, чтобы избавиться от операции взятия остатка, достаточно использовать 3 генератора с диапазонами [1;2] и предыдущий алгоритм.
Свести диапазон [1;6] к [1;2] можно простым делением на 3.
Сужение диапазона приводит к потери части информации и необходимости генерации большего объёма случайностей.
В общем случае (для произвольного количества состояний выхода), возможно использование разного основания системы для разных разрядов. Эту часть алгоритма (выбор разбиения на множители) можно автоматизировать.
Самый лучший алгоритм (в смысле соответствия выходной последовательности равномерному распределению) - самый же медленный. При этом, в отдельных случаях (например, при кратности диапазона генератора диапазону кубика: [1;12]) второй алгоритм будет выдавать такую же по качеству последовательность, используя меньшее число бросков.
Если же диапазон генератора кратен простому числу, не являющемуся множителем исходного диапазона игральной кости, то подобрать коэффициенты для реализации алгоритма не удастся, так как не получится построить разбиение на множители. Например число 9 кратно простому числу 3, которое является множителем для 6, а вот число 14 - кратно 7, которое никак из шестигранного кубика не получить. Исключение (для произвольной кости) - игральная кость изначально имеет простое число граней. Но как реализовать симметричную (для равновероятности выпадения) стереометрическую фигуру, имеющую нечётное количество граней? Я о таких игральных костях не слышал, а даже если они есть - то "выудить" из них можно будет только один множитель.
При невозможности синтезировать разбиение на множители, можно выбрать ближайший больший диапазон (для 14 это 15=3×5) и отбрасывать значения, большие верхней границы генератора (15). Оставшиеся числа будут распределены равномерно. И хотя мы можем оценить среднее количество таких "бракованных" бросков, подобным допущением мы нарушаем исходные условия задачи (фиксированное количество действий).
Негативный эффект от использования операции взятия остатка от деления можно нивелировать, если исходная величина существенно превосходит делитель (тут - или исходный генератор с большим диапазоном, или больше бросков). Например, при сужении диапазона [1;100] к [1;3], повышение вероятности у первого варианта будет всего-лишь в 34/33≈1.03 раза.
На этом всё - бросайте игральные кости правильно!
Если уж заниматься ерундой, то подойти к ней надо с умом
- сериал «С приветом по планетам»; эпизод «Героический подвиг вселенского масштаба»
Постановка задачи
Есть шестигранный кубик (с равными вероятностями выпадения сторон). Необходимо получить при помощи это кубика N отсчётов дискретного равномерного белого шума с диапазоном значений [1;8]. Получение одного отсчёта должно выполняться за фиксированное количество действий. Описать алгоритм получения одного отсчёта.
Иными словами, получаемые с генератора значения должны быть равновероятны (то есть иметь равномерное распределение) и не зависеть от предшествующих состояний генератора (шум должен быть белым, то есть его автокорреляционная функция должна иметь вид δ-функции Дирака). Ну и - исходя из физической природы случайности (игральной кости), на которой работает наш более сложный генератор - выходная величина должна изменяться дискретно (никаких "2,5" и тому подобного).
Дискретность значений и необходимый вид функции автокорреляции гарантирует природа игральной кости. (Впрочем, это несложно испортить неудачным алгоритмом использования кубика.) Осталось разобраться с равномерностью распределения значений.
Экспериментальная установка
Игральные кости (с фотографии) уже убраны в коробку: для серьёзной работы такой инструмент не годится.
Для тестирования алгоритма генерации я буду использовать полюбившийся мне за годы эксплуатации метод математического моделирования. Эксперимент заключается в многократном повторении моделирования эпизода работы генератора. При достаточно большом количестве итераций, экспериментальный результат будет соответствовать аналитическому. Тем самым будет подтверждена корректность теоретических выкладок. Построить эксперимент подобным образом для данного типа задач, можно опираясь на Закон больших чисел:
Эмпирическое среднее (среднее арифметическое) достаточно большой конечной выборки из фиксированного распределения близко к теоретическому среднему (математическому ожиданию) этого распределения.
Подробнее о методе Монте-Карло смотри здесь.
Необходимое количество итераций прикинем "на глаз", опираясь на динамику результатов и аналитику.
Опишем программную реализацию кубика с шестью гранями. Попутно будем считать количество вызовов (бросков кости), чтобы оценить сложность алгоритма.
Решение на языке BlitzBasic
1234 | Function MyRand%() Calls=Calls+1 Return Rand(1,6) End Function |
Используемая здесь функция
Rand
Тестовый запуск
Определим нулевой вариант решения, реализация которого нужна для тестирования работы установки.
Решение на языке BlitzBasic
123 | Function Get0%() Return MyRand() End Function |
Представленный алгоритм
Get0
Как видно из рисунка, для генерации миллиона значений потребовался миллион бросков. Каждое число выпадало примерно одинаковое количество раз (3-яя снизу строка). Повторяя эксперимент, можно получить превалирование то одного, то другого исхода.
Алгоритм с аккумуляцией случайности
Как правило, это решение приводят первым. Сводится оно к тому, что кубик бросается несколько раз, при этом количество выпавших очков суммируется. Число бросков заранее оговаривается: его выбирают таким, чтобы максимальная сумма (с учётом коррекции) выпавших очков была не меньше правой границы генератора. Так как при помощи игральной кости нельзя выбросить "ноль очков", то сумма корректируется (с учётом левой границы генератора) соответствующим уменьшением. Если подобрать число бросков идеально не получается, и результирующая сумма превосходит максимальное выходное значение генератора, то от суммы берётся остаток от деления.
Решение на языке BlitzBasic
123456789101112131415 | Function GetA%() Local RndGenPow%=6 Local Max%=8 Local Top%=Ceil(Max/Float(RndGenPow)) Local S%=0 Local i% For i=1 To Top S=S+MyRand() Next S=S-Top S=S Mod Max S=S+1 Return S End Function |
В нашем случае, для генерации понадобится два броска кубика (сумма может принимать значения от 2 до 12 включительно). Затем будет произведено вычитание двойки - сумма сдвинется до [0; 10]. Далее взятие остатка от деления - [0; 7]. И финальная коррекция - [1; 8].
Это ужасный алгоритм! Первое, на что стоит обратить внимание: это использование операции взятия остатка от деления. В случае, если мы берём остаток от деления на число, которое не кратно максимальному значению делимому числа, то мы получим "перекос" в распределении.
Действительно: числа 0, 1, 2, 3, 4, 5, 6, 7 - остаются на "своих местах", а числа 8, 9, 10 - преобразуются соответственно в 0, 1, 2. Вероятность выпадения первых трёх чисел возрастает.
Но это ещё не всё. Центральная предельная теорема говорит о том, что:
Сумма достаточно большого количества слабо зависимых случайных величин, имеющих примерно одинаковые масштабы (ни одно из слагаемых не доминирует, не вносит в сумму определяющего вклада), имеет распределение, близкое к нормальному.
Все условия для наблюдения эффекта соблюдены.
Действительно: мы пытаемся свести 6×6=36 внутренних состояний генератора к 8-ми выходным значениям. Для сохранения равномерного распределения необходимо, чтобы каждое значение из [1; 8] можно было получить одинаковым количеством способов, а именно: 36/8=4,5. Уже нецелое число в ответе должно насторожить, но, чтобы окончательно убедиться в перекосах: минимальное число можно получить единственным способом. Последнее, правда, несколько компенсируется другим негативным эффектом (остатком от деления).
Суперпозиция эффектов порождает интересное распределение.
Основной негативный эффект (по-большому счёту, затмевающий перекос из-за использования остатка от деления) создаёт стремление получающегося распределения к распределениею Гаусса (как и ожидалось, исходя из Ц. П. Т.).
Для генерации понадобилось 2 миллиона бросков.
Алгоритм с системой счисления с основанием 6
Заменив обычное суммирование взвешенной суммой, мы уйдём от условий, благоприятных для образования нормального распределения. В качестве взвешенной суммы, будем интерпретировать каждый бросок как цифру в некоей позиционной системе счисления. Очевидно, в данном случае, логично выбрать основание 6.
К аналогичному решению проще прийти из комбинаторных соображений.
Решение на языке BlitzBasic
123456789101112131415 | Function GetB%() Local RndGenPow%=6 Local Max%=8 Local Top%=Ceil(Log(Max)/Log(RndGenPow)) Local S%=0 Local i% For i=1 To Top S=S+(MyRand()-1)*(6^(i-1)) Next S=S Mod Max S=S+1 Return S End Function |
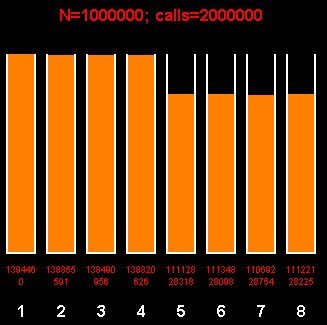
Тем не менее, операция взятия остатка от деления осталась. Алгоритм плох! Так как 36/8=4,5, то можно предположить, что будет увеличена вероятность для 36-8*4=4-ых первых исходов, а отношение величин будет приблизительно (4+1)/4=5/4.
Предсказанное сбылось:
5/4=1,25
139446/111128≈1,25482...
Алгоритм с системой счисления с переменным основанием
Нетрудно заметить, что искомое число комбинаций представимо в виде произведения 8=2×2×2. (Здесь уместна аналогия: случайно выбираем половину интервала, затем делим её на две части и снова делаем случайный выбор и так далее.) Таким образом, чтобы избавиться от операции взятия остатка, достаточно использовать 3 генератора с диапазонами [1;2] и предыдущий алгоритм.
Свести диапазон [1;6] к [1;2] можно простым делением на 3.
Решение на языке BlitzBasic
1234567891011121314151617 | Function GetC%() Local RndGenPow%=6 Local S%=0 Local n%=3 Local div%[3] Local pow%[3] div[1]=3:div[2]=3:div[3]=3 Local i% For i=1 To n pow[i]=RndGenPow/div[i] Next For i=1 To n S=S+Floor((MyRand()-1)/div[i])*(pow[i]^(i-1)) Next Return S+1 End Function |
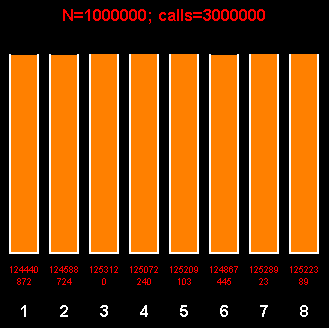
Сужение диапазона приводит к потери части информации и необходимости генерации большего объёма случайностей.
В общем случае (для произвольного количества состояний выхода), возможно использование разного основания системы для разных разрядов. Эту часть алгоритма (выбор разбиения на множители) можно автоматизировать.
Выводы и примечания
Самый лучший алгоритм (в смысле соответствия выходной последовательности равномерному распределению) - самый же медленный. При этом, в отдельных случаях (например, при кратности диапазона генератора диапазону кубика: [1;12]) второй алгоритм будет выдавать такую же по качеству последовательность, используя меньшее число бросков.
Если же диапазон генератора кратен простому числу, не являющемуся множителем исходного диапазона игральной кости, то подобрать коэффициенты для реализации алгоритма
GetC
При невозможности синтезировать разбиение на множители, можно выбрать ближайший больший диапазон (для 14 это 15=3×5) и отбрасывать значения, большие верхней границы генератора (15). Оставшиеся числа будут распределены равномерно. И хотя мы можем оценить среднее количество таких "бракованных" бросков, подобным допущением мы нарушаем исходные условия задачи (фиксированное количество действий).
Негативный эффект от использования операции взятия остатка от деления можно нивелировать, если исходная величина существенно превосходит делитель (тут - или исходный генератор с большим диапазоном, или больше бросков). Например, при сужении диапазона [1;100] к [1;3], повышение вероятности у первого варианта будет всего-лишь в 34/33≈1.03 раза.
На этом всё - бросайте игральные кости правильно!



Комментарии