Вероятность не угадать всё
Просмотров: 2462
06 февраля 2016 года
Иногда случайные слова из мешочка с диалогом могут до жути подходить к описанию событий и придавать им особый жуткий смысл.
- Роберт Шекли. Машина Шехерезада. История четвертая «Джордж и коробки».
Новые Миры Роберта Шекли. Т. 2 /Пер. с англ. — Рига: Полярис, 1996. — 367 с.
Встречаются игры и пари в духе "угадай: под каким напёрстком шарик". Логично предположить, что если игрок почти всегда из двух напёрстков выбирает "не тот", то ему просто надо скорректировать тактику и выбирать "неправильный" по его мнению. С формальной точки зрения, существуют лишь вероятности того или иного исхода, лишённые какой-либо эмоциональной окраски. Могут ли отдельные проигрышные ситуации в игре со случайным выбором быть менее вероятными, чем победа? В таком случае, можно было бы говорить о своеобразном "везении в проигрыше", который можно трансформировать в везение (в привычном понимании), переформулировав (для себя) правила игры.
Постановка задачи
После нескольких итераций обтёсывания условий, я получил следующее описание одной из игр.
Перед Вами N пронумерованных корзин и мешочек, содержащий N одинаковых по весу, объёму и фактуре шаров. На каждый шар особым образом нанесён уникальный номер от 1 до N: шар может быть развинчен на две половинки, на внутренних поверхностях которых и нанесён номер. Вы достаёте шары вслепую. Выбрав на своё усмотрение шар из мешочка, Вы указываете в какую корзину он будет положен (в каждую корзину - только один шар). Шары обратно не возвращаются, а номера шаров оглашаются после заполнения последней корзины. Какова вероятность того, что выложенные наудачу шары окажутся разложенными полностью неверно: то есть ни один шар не будет лежать в "своей" корзине?
Здесь игрок совершает выбор, нацеленный на восстановление неких пар "корзина-шар". Условия подразумевают, что играющий делает выбор случайно, так как не располагает какой-либо информацией, проясняющей ситуацию. Даже особый способ маркировки шаров нужен для того, чтобы не дать игроку сформировать тактику выбора корзин, строя предположения об оставшихся в мешочке номерах. (Впрочем, в силу бихевиористичности "испытания", удачное угадывание может имитировать доступ к подобной информации.)
Аналитическое решение
После первого же шара на своём месте (с чёрным номером) комбинация бракуется
Если мы выставим корзины в ряд (например, в порядке возрастания номеров), то после вытаскивания последнего шара, мы будем иметь числовую последовательность, соответствующую номерам разложенных по корзинам шаров. В конечном счёте, именно комбинация номеров и является кодом, определяющим удачность того или иного расклада.
Вероятность наступления означенного выше события будет выражаться как "удачное" (то есть удовлетворяющее условию задачи) количество комбинаций шаров к общему количеству комбинаций.
Сначала рассмотрим общее количество комбинаций. Решение тривиальное: первый шар мы можем разместить в одной из N корзин, после чего второй - в одной из (N-1), и так далее. Таким образом, общее количество выражается как N*(N-1)*(N-2)*…*2*1. Данное выражение более известно как факториал:
В свою очередь, мы показали вывод формулы для подсчёта количества "размещений из n по n" или количества "перестановок порядка n".
В комбинаторике размещением (из n по k) называется упорядоченный набор из k различных элементов из некоторого множества различных n элементов.
В комбинаторике перестановка — это упорядоченный набор чисел 1, 2, …, n, обычно трактуемый как биекция на множестве {1, 2, …, n}, которая числу i ставит в соответствие i-й элемент из набора.
Сложности начинаются при попытке оценить количество удачных комбинаций. "Удачные" здесь это те, в которых ни один шар не лежит в нужной корзине.
Вычислить количество таких комбинаций можно разными путями.
Оценить количество удачных раскладов непосредственно. Первый шар мы можем разместить (N-1) способом (ещё один способ соответствует выбору правильной корзины). Но из этого умозаключения не следует, что второй шар имеет (N-2) вакантных корзины. В самом деле: при N=3, в зависимости от того, куда будет положен первый шар (пусть с №2) и второй шар (пусть с №1), мы можем получить как удачную, так и неудачную комбинацию. Например, №2 мы положим в первую корзину, а №1 - во вторую, после это шар №3 априори окажется в корзине №3, что делает комбинацию неудачной. С другой стороны, №2 можно положить в третью корзину, а №1 - во вторую, после этого шар №3 априори окажется в корзине №1, образуя удачную комбинацию. Простых идей "как учесть взаимовлияние" у меня нет.
Оценить количество неудачных раскладов. Надо оценить количество комбинаций, соответствующих событиям "верно выбрана одна корзина, а остальные шары - как получится" (p=(N-1)!), "верно выбраны две корзины, а остальные, (N-2) шаров - могут быть не на своих местах" (p=(N-2)!), и т.д. Зная количество комбинаций для указанных событий, общее количество комбинаций, и количество комбинаций "все шары на своих на местах" (одна) - можно вычислить количество раскладов для искомого события "все мимо". Проблема подхода кроется в том, перечисленные события не являются несовместными.
В теории вероятностей несколько событий называются несовместными, если никакие из них не могут появиться одновременно в результате однократного проведения эксперимента (опыта).
Предположим, что шар №1 угадан верно. А теперь представим расклад, где угаданы корзины для шаров №1 и №2. В виду сложности, мы не поставили для первого случая исключение на угадывание и корзины №2 - таким образом, множество комбинаций, удовлетворяющих первому событию, включает себя и множество комбинаций для второго события.
Необходимо рассматривать события типа "верно выбрано k корзин, а остальные (N-k) - заполнены гарантированно неправильно". Но тут возникают сложности из предыдущего способа (взаимовлияние).
На самом деле - нам нужно вычислить количество всех "беспорядков порядка N":
Можно не изобретать велосипед и воспользоваться готовым решением, полученным с помощью принципа включения-исключения:
комбинаторная формула, позволяющая определить мощность объединения конечного числа конечных множеств, которые в общем случае могут пересекаться друг с другом
Искомое число находится по формуле:
Собрав всё воедино, получим вот такую забавную формулу ("субфакториал N делить на факториал N"):
Решение методом Монте-Карло
Для конкретики выберем N=10 и посчитаем значение по формуле.
Решение на MATLAB
1234 | N=10; K=0:N; Pk=((-1).^K)./factorial(K); P=sum(Pk) |
Для того, чтобы MATLAB "правильно понял", что именно нужно делать (и не начал использовать матричные операторы), приходится использовать поэлементное возведение в степень и поэлементное деление.
Результат P≈0.3679.
Мне было лень возиться с проектом для Си++, поэтому моделирование эксперимента снова на Blitz:
Решение на языке BlitzBasic (основная часть)
123456789101112131415161718192021222324252627282930313233 | Const ZTotal%=2000000 Const N%=10 Local i%,Z%,Zok% Dim V%(N) For i=1 To N V(i)=i Next Zok=0 For Z=1 To ZTotal For i=1 To N^2 Local a_indx%=Rand(1,N) Local b_indx%=((a_indx+Rand(1,N-1)-1) Mod N)+1 Local t%=V(a_indx) V(a_indx)=V(b_indx) V(b_indx)=t Next Local Ok%=True;все не так For i=1 To N If V(i)=i Ok=False Exit EndIf Next If Ok Then Zok=Zok+1 Next |
Для генерации перестановок я использовал цикл с N2 транспозициями исходного массива (моделирующего вариант размещения шаров по корзинам) для каждого эксперимента. Используемый алгоритм выбора элементов разбирался ранее. Для каждого следующего эксперимента перемешивался используемый на прошлой итерации массив, а не начальный.
Искомая вероятность вычисляется как:
Решение на языке BlitzBasic (вероятность)
1 | Zok/Float(ZTotal)
|
Сделаем два запуска:
| Количество повторений | Вычисленная вероятность |
| 2000000 | 0.367997 |
| 10886400 (в 3 раза больше, чем существует комбинаций) | 0.368068 |
Как можно заметить, результаты, полученные методом Монте-Карло, согласуются с аналитическим решением.
Вывод
Для рассмотренной задачи (10 шаров), вероятность не угадать корзины для всех шаров сразу - не так уж и мала (почти 40%), как может показаться на интуитивном уровне.
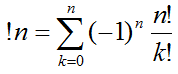
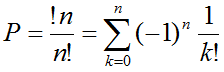
Комментарии