Способы интеллектуальной поддержки пилота летательного аппарата на основе концепции треугольника мощности
Просмотров: 1872
2016 год
Корсун О.Н., Бурлак Е.А., Набатчиков А.М., Харьков В.П. Способы интеллектуальной поддержки пилота летательного аппарата на основе концепции треугольника мощности // Труды ГосНИИАС. ВОПРОСЫ АВИОНИКИ. – М.: ГосНИИАС, 2016. – №26. – С.18-24.
УДК: 629.735:004.9
Предлагается новый подход к индикации предельных значений параметров полета летательного аппарата на основе баланса энергий и на рассмотрении таких параметров полета как скорость, углы наклона траектории θ и крена γ.
В статье рассматривается новый подход к расчету и индикации основных параметров, определяющих траекторное движение летательного аппарата использующий концепцию треугольника мощности, основанного на балансе энергий ЛА и двигателя [1]. Достоинством предлагаемой идеи является наглядность представления предельных значений углов тангажа, крена и скорости полета и соотношений между ними, которая повышает эффективность деятельности летчика пилотируемого ЛА и степень его информированности о параметрах движения ЛА. Особенность предлагаемых решений заключается в том, что явно рассматриваются только три вышеуказанных параметра (скорость, тангаж, крен). Угол атаки, сила аэродинамического сопротивления, сила тяги двигателя учитываются неявно, при расчете основных соотношений динамики движения летательного аппарата. Другая особенность состоит в том, что рассматривается класс маневров, выполняемых без скольжения (с около нулевыми углами скольжения).
Далее в статье рассматриваются только основные концептуальные положения предлагаемого подхода. Отработку конкретных решений и их апробацию планируется выполнить в ходе полунатурного моделирования на пилотажно-исследовательском стенде, разработанным авторским коллективом [2, 3].
Решение задачи автоматического управления вектором скорости полета летательного аппарата (ЛА) предполагает, что параметры движения не выходят за пределы эксплуатационных ограничений. В противном случае необходимо предусмотреть коррекцию управляющих воздействий, приводящих ЛА в зону допустимых или разрешенных изменений координат состояния. Наиболее значимой координатой состояния, влияющей на безопасность полета, является вектор скорости полета. В этом случае необходимо так управлять ЛА и его силовой установкой, чтобы всегда выполнялось условие:
где Vmin = Vmin(H), Vmax = Vmax(H) - минимальное и максимальное значения скорости полета, определяемое эксплуатационным диапазоном высот и скоростей полета.
Учитывая, что ЛА может выполнять в пространстве состояния сложные маневры с различными фиксированными значениями некоторых координат, например, скорость полета V, угол наклона траектории θ, высота полета H и т.д., то левая и правая границы допустимого диапазона изменения скорости полета представляют собой сложные функции как координат состояния, так и располагаемых энергетических ресурсов. В зависимости от стратегии управления ЛА будет зависеть и решение задачи ограничения скорости полета. Под стратегией управления здесь понимается разрешенные способы влияния на скорость полета: изменения траектории полета, изменения тяги силовой установки, изменения лобового сопротивления ЛА, любая комбинация перечисленных выше способов управления. Естественно полагать, что комбинированный способ управления является наиболее эффективным и предпочтительным.
Вектор скорости в полярной системе координат определяется следующими параметрами:
Исходя из располагаемых ресурсов, допустимых органов управления скоростью на данном режиме и от принятой стратегии ограничения контролируемой координаты, система управления может строиться по двум принципам:
Здесь под «энергетическими» координатами понимаются прежде всего углы наклона траектории θ и крена γ, которые при заданной скорости полета для реализации некоторых их назначений требуют дополнительного расхода энергетических ресурсов – тяги силовой установки. При чем большим реализуемым значениям θ и γ соответствуют и большие дополнительные расходы тяги силовой установки.
Предполагается, что в качестве располагаемых органов управления могут использоваться как тяга силовой установки, так и аэродинамический руль высоты – стабилизатор.
В качестве базового режима полета примем полет на заданной высоте Но с произвольным, но зафиксированным значением скорости Vo. Этому режиму соответствует некоторое значение тяги Ро силовой установки. Предположим, что ЛА совершает разворот за счет изменения углов крена. Для поддержания заданной высоты полета необходимо увеличить угол атаки. При этом скорость полета несколько уменьшается за счет увеличения лобового сопротивления. В этом случае тяга Ро расходуется на поддержание новой скорости V1 и на создание некоторого угла крена γ ≠ 0.
Дальнейшее увеличение крена приведет к уменьшению скорости полета до значения, равного:
при условии стабилизации высоты полета Но = const.
Если по условию полетного задания требуется продолжить увеличивать угол крена, то для сохранения равенства (2) необходимо увеличивать тягу силовой установки.
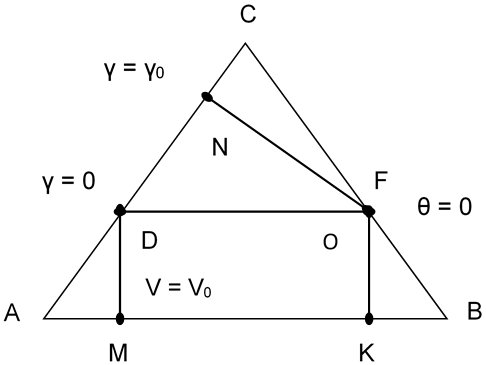
Для геометрической интерпретации изложенного воспользуемся равносторонним треугольником, который в дальнейшим будем называть треугольником мощности. Высоту треугольника будем интерпретировать как величину тяги силовой установки. По сторонам треугольника в некотором масштабе отложены значения V, γ и θ. Воспользуемся свойством равностороннего треугольника – сумма перпендикуляров, отложенных из произвольной внутренней точки на стороны, есть величина постоянная и равная высоте треугольника. Тогда можно утверждать, что длины перпендикуляров, опущенные на стороны треугольника, пропорциональны текущим значениям частям тяги, необходимых для создания V, γ и θ. В качестве примера треугольник мощности для режима полета: V(t) = V0, Н(t)=H0=const, |γ(t)|=|γ0| представлен на рис. 1
Здесь обозначено:
Точка О называется равновесной точкой, положение которой и определяет возможные значения координат V, γ и θ. На рис.1 точка О совпадает с F. Это означает, что в данном случае полет с набором высоты невозможен.
Заметим, что высота h треугольника здесь удовлетворяет условию:
и определяется по высотно-скоростным характеристикам (ВСХ) и дроссельным характеристикам двигателя. Масштаб по координатам V, γ и θ является нелинейным и в общем случае зависит от веса ДПЛА, высоты и числа М полета.
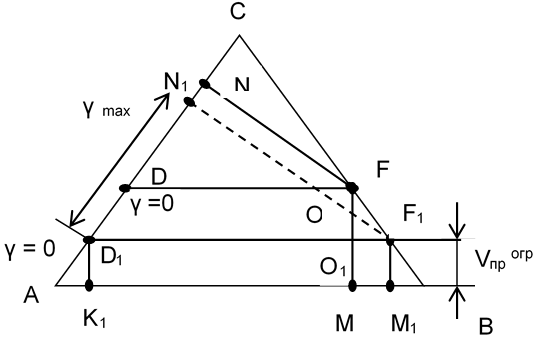
На рис. 2 изображен тот же треугольник мощности, что и на рис.1, на котором дополнительно показано:
Из рисунка следует, что в этом случае равновесная точка переместилась из точки О в точку О1. Дальнейшее увеличение крена приведет к нарушению условия:
Следовательно, необходимо формировать корректирующий сигнал, направленный на ограничение заданного угла крена, либо на увеличение тяги силовой установки.
Принадлежность фигуративной точки внутренней части треугольника мощностей АВС означает, что все управляемые координаты не равны нулю.
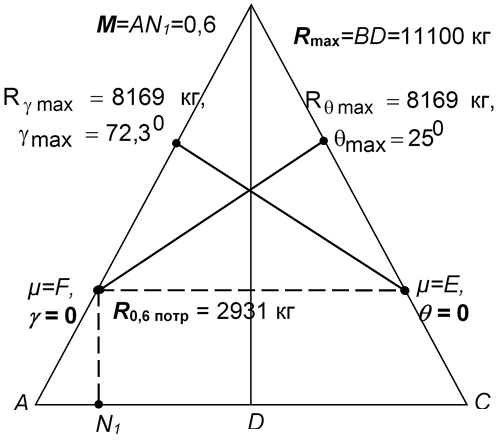
На рисунке 3 приведен текущий треугольник мощностей для средне магистрального судна для двух ситуаций, когда полет совершается с набором высоты и с разворотом. Из рисунка 3 следует, что полет совершается на высоте H = 2000 м со скоростью полета M = 0,6 и углами крена γ = 0, наклона траектории θ = 25°, если фигуративная точка μ совпадает с точкой F ∈ AB. Если же фигуративная точка μ совпадает с точкой E ∈ BC, то параметры полета соответственно равны H = 2000 м, M = 0,6, θ = 0 и γ = 72,3°. При этом распределение энергетических ресурсов по контурам управления распределяется следующим образом:
а) μ = F ∈ AB
Положение δруд соответствует частоте вращения nk = 100 %. Тяга, развиваемая силовой установкой на данном режиме составляет R=BD=11100 кг. Заметим, что для обоих случаев условие (2) выполняется. Сумма составляющих тяги, распределяемых отдельным контурам RV+Rθ+Rγ, должна быть равна тяге R создаваемой силовой установкой. Подставляя конкретные значения тяги для данных параметров полета получим:
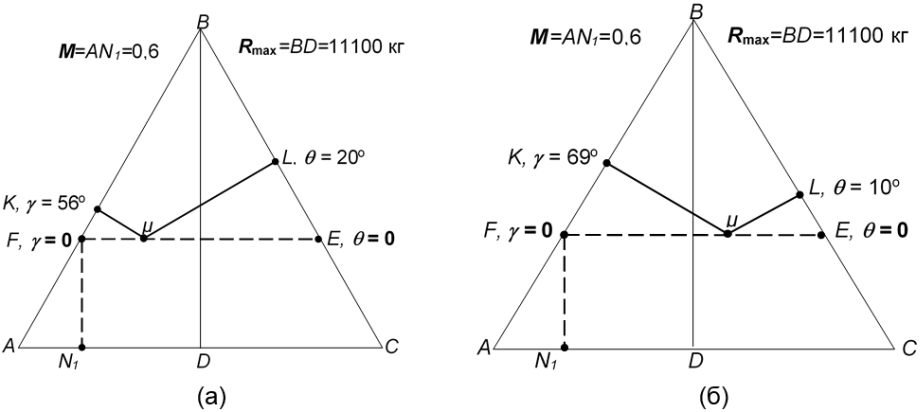
На рисунке 4 изображены две ситуации, когда фигуративная точка лежит внутри треугольника мощностей АВС. Распределение тяги между контурами при полете на высоте H = 2000 м и со скоростью M = 0,6 и углами θ = 20°, γ = 56° показано на рисунке 4(а), а с углами θ = 10°, γ = 69° на рисунке 4(б). Здесь, как и прежде основой является выполнение условия (2). Исходя из рисунка 4 действительно имеем:
а) RV+Rθ+Rγ = 2931 кг + 6609 кг + 1560 кг = 11100 кг = R;
б) RV+Rθ+Rγ = 2931 кг + 3371 кг + 4792 кг = 11100 кг = R.
Правило построения и основные свойства предельного треугольника мощностей рассмотрено в [1].
Области использования данного подхода:
Рассмотренный выше подход предполагается осуществлять путем предъявления треугольника на рабочий экран оператора ДПЛА.
Для проведения экспериментов предполагается использовать разработанный авторским коллективом аппаратно-программный стенд для моделирования пилотируемого полета в целях отработки систем управления и тестирования алгоритмов и программы анализа полетных данных [2,3].
Преимущество метода заключается в обеспечении наглядной и образной индикации предельных значений параметров полета (углов тангажа, крена и скорости полета) и соотношений между ними, что облегчает оператору ДПЛА (летчику пилотируемого ЛА) формирование образа полета и оценивание возможностей маневрирования без превышения предельных допустимых значений полетных параметров.
Работа выполнена при поддержке Российского Фонда фундаментальных исследований (РФФИ), проект № 14-08-01109-а.
A new approach to indicate the limit values of the aircraft on the basis of the energy balance and consideration of parameters such as the flight path angles θ and roll γ, that is, the coordinates of the state vector
В статье рассматривается новый подход к расчету и индикации основных параметров, определяющих траекторное движение летательного аппарата использующий концепцию треугольника мощности, основанного на балансе энергий ЛА и двигателя [1]. Достоинством предлагаемой идеи является наглядность представления предельных значений углов тангажа, крена и скорости полета и соотношений между ними, которая повышает эффективность деятельности летчика пилотируемого ЛА и степень его информированности о параметрах движения ЛА. Особенность предлагаемых решений заключается в том, что явно рассматриваются только три вышеуказанных параметра (скорость, тангаж, крен). Угол атаки, сила аэродинамического сопротивления, сила тяги двигателя учитываются неявно, при расчете основных соотношений динамики движения летательного аппарата. Другая особенность состоит в том, что рассматривается класс маневров, выполняемых без скольжения (с около нулевыми углами скольжения).
Далее в статье рассматриваются только основные концептуальные положения предлагаемого подхода. Отработку конкретных решений и их апробацию планируется выполнить в ходе полунатурного моделирования на пилотажно-исследовательском стенде, разработанным авторским коллективом [2, 3].
Решение задачи автоматического управления вектором скорости полета летательного аппарата (ЛА) предполагает, что параметры движения не выходят за пределы эксплуатационных ограничений. В противном случае необходимо предусмотреть коррекцию управляющих воздействий, приводящих ЛА в зону допустимых или разрешенных изменений координат состояния. Наиболее значимой координатой состояния, влияющей на безопасность полета, является вектор скорости полета. В этом случае необходимо так управлять ЛА и его силовой установкой, чтобы всегда выполнялось условие:
Vmin ≤ V(t) ≤ Vmax (1)
где Vmin = Vmin(H), Vmax = Vmax(H) - минимальное и максимальное значения скорости полета, определяемое эксплуатационным диапазоном высот и скоростей полета.
Учитывая, что ЛА может выполнять в пространстве состояния сложные маневры с различными фиксированными значениями некоторых координат, например, скорость полета V, угол наклона траектории θ, высота полета H и т.д., то левая и правая границы допустимого диапазона изменения скорости полета представляют собой сложные функции как координат состояния, так и располагаемых энергетических ресурсов. В зависимости от стратегии управления ЛА будет зависеть и решение задачи ограничения скорости полета. Под стратегией управления здесь понимается разрешенные способы влияния на скорость полета: изменения траектории полета, изменения тяги силовой установки, изменения лобового сопротивления ЛА, любая комбинация перечисленных выше способов управления. Естественно полагать, что комбинированный способ управления является наиболее эффективным и предпочтительным.
Вектор скорости в полярной системе координат определяется следующими параметрами:
- модулем скорости V(t);
- углами наклона траектории и курсовым углом.
Исходя из располагаемых ресурсов, допустимых органов управления скоростью на данном режиме и от принятой стратегии ограничения контролируемой координаты, система управления может строиться по двум принципам:
- компенсационный принцип управления;
- принцип энергетического управления.
Здесь под «энергетическими» координатами понимаются прежде всего углы наклона траектории θ и крена γ, которые при заданной скорости полета для реализации некоторых их назначений требуют дополнительного расхода энергетических ресурсов – тяги силовой установки. При чем большим реализуемым значениям θ и γ соответствуют и большие дополнительные расходы тяги силовой установки.
Предполагается, что в качестве располагаемых органов управления могут использоваться как тяга силовой установки, так и аэродинамический руль высоты – стабилизатор.
В качестве базового режима полета примем полет на заданной высоте Но с произвольным, но зафиксированным значением скорости Vo. Этому режиму соответствует некоторое значение тяги Ро силовой установки. Предположим, что ЛА совершает разворот за счет изменения углов крена. Для поддержания заданной высоты полета необходимо увеличить угол атаки. При этом скорость полета несколько уменьшается за счет увеличения лобового сопротивления. В этом случае тяга Ро расходуется на поддержание новой скорости V1 и на создание некоторого угла крена γ ≠ 0.
Дальнейшее увеличение крена приведет к уменьшению скорости полета до значения, равного:
V(t) = Vпрогр (2)
при условии стабилизации высоты полета Но = const.
Если по условию полетного задания требуется продолжить увеличивать угол крена, то для сохранения равенства (2) необходимо увеличивать тягу силовой установки.
Для геометрической интерпретации изложенного воспользуемся равносторонним треугольником, который в дальнейшим будем называть треугольником мощности. Высоту треугольника будем интерпретировать как величину тяги силовой установки. По сторонам треугольника в некотором масштабе отложены значения V, γ и θ. Воспользуемся свойством равностороннего треугольника – сумма перпендикуляров, отложенных из произвольной внутренней точки на стороны, есть величина постоянная и равная высоте треугольника. Тогда можно утверждать, что длины перпендикуляров, опущенные на стороны треугольника, пропорциональны текущим значениям частям тяги, необходимых для создания V, γ и θ. В качестве примера треугольник мощности для режима полета: V(t) = V0, Н(t)=H0=const, |γ(t)|=|γ0| представлен на рис. 1
Здесь обозначено:
- ОМ – перпендикуляр, опущенный из точки О на сторону АВ треугольника, длина которого пропорциональна тяге, потребной для создания скорости V = V0;
- DK – отрезок, пропорциональный величине скорости V(t) = V0;
- ON – перпендикуляр, опущенный из точки О на сторону АС, на которой нанесен масштаб угла крена. Его длина пропорциональна необходимой дополнительной тяге для создания крена, равного |γ0| при V = V0 и H=const;
- DN – отрезок, величина которого пропорциональна крену |γ(t)|. Начало отсчета по крену принимается в точке D, определяемая как точка пересечения прямой DF||AB со стороной AC.
Точка О называется равновесной точкой, положение которой и определяет возможные значения координат V, γ и θ. На рис.1 точка О совпадает с F. Это означает, что в данном случае полет с набором высоты невозможен.
Заметим, что высота h треугольника здесь удовлетворяет условию:
||h||= ||OM|| + ||ON||
и определяется по высотно-скоростным характеристикам (ВСХ) и дроссельным характеристикам двигателя. Масштаб по координатам V, γ и θ является нелинейным и в общем случае зависит от веса ДПЛА, высоты и числа М полета.
На рис. 2 изображен тот же треугольник мощности, что и на рис.1, на котором дополнительно показано:
- D1K1 – минимально возможная скорость полета, равная Vпрогр;
- D1N1 – максимально возможный угол крена на данном режиме работы силовой установки при стабилизации высоты полета.
Из рисунка следует, что в этом случае равновесная точка переместилась из точки О в точку О1. Дальнейшее увеличение крена приведет к нарушению условия:
Vпр(t) ≥ Vпрогр.
Следовательно, необходимо формировать корректирующий сигнал, направленный на ограничение заданного угла крена, либо на увеличение тяги силовой установки.
Принадлежность фигуративной точки внутренней части треугольника мощностей АВС означает, что все управляемые координаты не равны нулю.
На рисунке 3 приведен текущий треугольник мощностей для средне магистрального судна для двух ситуаций, когда полет совершается с набором высоты и с разворотом. Из рисунка 3 следует, что полет совершается на высоте H = 2000 м со скоростью полета M = 0,6 и углами крена γ = 0, наклона траектории θ = 25°, если фигуративная точка μ совпадает с точкой F ∈ AB. Если же фигуративная точка μ совпадает с точкой E ∈ BC, то параметры полета соответственно равны H = 2000 м, M = 0,6, θ = 0 и γ = 72,3°. При этом распределение энергетических ресурсов по контурам управления распределяется следующим образом:
а) μ = F ∈ AB
- RV =2931 кг – тяга силовой установки, необходимая для создания скорости полета M = 0,6 на высоте H = 2000 м;
- Rθ = 8169 кг – тяга, необходимая для полета с углом наклона траектории θ = 25° и скоростью полета M = 0,6 на высоте H = 2000 м;
- Rγ = 0 кг – потребная тяга для полета на высоте H = 2000 м с параметрами: M = 0,6, θ = 25°, γ = 0;
Положение δруд соответствует частоте вращения nk = 100 %. Тяга, развиваемая силовой установкой на данном режиме составляет R=BD=11100 кг. Заметим, что для обоих случаев условие (2) выполняется. Сумма составляющих тяги, распределяемых отдельным контурам RV+Rθ+Rγ, должна быть равна тяге R создаваемой силовой установкой. Подставляя конкретные значения тяги для данных параметров полета получим:
2931 кг + 8169 кг + 0 кг = 11100 кг
или
или
На рисунке 4 изображены две ситуации, когда фигуративная точка лежит внутри треугольника мощностей АВС. Распределение тяги между контурами при полете на высоте H = 2000 м и со скоростью M = 0,6 и углами θ = 20°, γ = 56° показано на рисунке 4(а), а с углами θ = 10°, γ = 69° на рисунке 4(б). Здесь, как и прежде основой является выполнение условия (2). Исходя из рисунка 4 действительно имеем:
а) RV+Rθ+Rγ = 2931 кг + 6609 кг + 1560 кг = 11100 кг = R;
б) RV+Rθ+Rγ = 2931 кг + 3371 кг + 4792 кг = 11100 кг = R.
Правило построения и основные свойства предельного треугольника мощностей рассмотрено в [1].
Области использования данного подхода:
- интеллектуальная поддержка действий оператора при управлении ДПЛА;
- интеллектуальная поддержка действий летчика пилотируемого ЛА;
- поддержка деятельности инженеров-разработчиков систем управления ЛА и инженеров-испытателей за счет наглядного и образного представления полетных ограничений ЛА и возможностей маневрирования.
Рассмотренный выше подход предполагается осуществлять путем предъявления треугольника на рабочий экран оператора ДПЛА.
Для проведения экспериментов предполагается использовать разработанный авторским коллективом аппаратно-программный стенд для моделирования пилотируемого полета в целях отработки систем управления и тестирования алгоритмов и программы анализа полетных данных [2,3].
Преимущество метода заключается в обеспечении наглядной и образной индикации предельных значений параметров полета (углов тангажа, крена и скорости полета) и соотношений между ними, что облегчает оператору ДПЛА (летчику пилотируемого ЛА) формирование образа полета и оценивание возможностей маневрирования без превышения предельных допустимых значений полетных параметров.
Работа выполнена при поддержке Российского Фонда фундаментальных исследований (РФФИ), проект № 14-08-01109-а.
Л И Т Е Р А Т У Р А
- O.N. KORSUN, V.P. HARKOV. Energy approach for aircraft velocity optimal control design. The 29th Congress of the International Council of the Aeronautical Sciences. St Petersburg, ICAS, 2014.
- КОРСУН О.Н., БУРЛАК Е.А., НАБАТЧИКОВ А.М. Исследовательский полунатурный стенд для анализа задач пилотирования и алгоритмов обработки полетных данных // Седьмой международный аэрокосмический конгресс IAC’2012. Сб. научн. тр. М.: 2013. 1 электрон. опт. диск (CD-ROM) рег. № 0321303652/03.06.2013.
- КОРСУН О. Н., НАБАТЧИКОВ А. М., БУРЛАК Е. А. Синхронизация информационных потоков при полунатурном моделировании движения летательных аппаратов // Электронный научно-технический журнал "Инженерный вестник", - 2013. - № 10. - С. 1-16.
METHODS OF INTELLECTUAL SUPPORT OF THE AIRCRAFT BASED ON THE TRIANGLE POWER CONCEPT
A new approach to indicate the limit values of the aircraft on the basis of the energy balance and consideration of parameters such as the flight path angles θ and roll γ, that is, the coordinates of the state vector
Файлы к скачиванию:
- Отсканированные страницы (3.71 МБ)

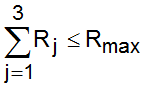
Комментарии