Две задачи о двух кубиках
Просмотров: 8528
24 мая 2016 года
Случается нередко нам
И труд и мудрость видеть там,
Где стоит только догадаться
За дело просто взяться.
И труд и мудрость видеть там,
Где стоит только догадаться
За дело просто взяться.
- И. А. Крылов «Ларчик».
И. А. Крылов. Сочинения в двух томах. Москва, «Государственное издательство художественной литературы», 1955. (Читать на Викитике.)
Несколько месяцев назад, коллега предложил мне две занятных задачи на применение теории вероятностей. Обе задачи в своих формулировках используют два шестигранных кубика и могут быть решены как очень сложно, так и элементарно. Итак.
Какова вероятность того, что на двух выброшенных кубиках будет дубль (то есть выпавшее на втором кубике значение будет равно первому)?
Какова вероятность того, что ни на одном из двух выброшенных кубиков не выпадет простое число?
Дубли
Первая задача кажется довольно примитивной, и после её прочтения в голове сразу складывается решение следующего вида.
Иными словами: вероятность равна отношению количества "удачных" исходов (n) к общему количеству (N) исходов эксперимента.
Очевидно, на руках у нас 2d6-генератор случайных чисел (то есть 2 игральные шестигранные кости), который может сгенерировать всего 6*6 или 62 вариантов.
Количество дублей - количество пар одинаковых значений первого и второго кубика. Очевидно, кубики образуют пары (1,1), (2,2), ..., (6,6) - таким образом, существует 6 возможных пар: для каждой грани первого кубика имеется такая же грань на втором.
Исходя из намеченного алгоритма решения, вычисляем результат n/N и обнаруживаем, что он равен 1/6.
На самом деле, обнаружив принцип образования пар (то есть интересующих нас исходов), можно прийти к выводу, что задача сводится к более простой формулировке:
Какова вероятность того, что на кубике выпадет загаданное число, входящее в диапазон возможных значений кубика?
Из этой формулировки несложно заключить, что искомая вероятность обратно пропорциональна числу граней в кубике. Задача, в общем-то, об одном кубике.
Простые числа
Оценив количество простых и "обычных" чисел, попробуем построить решение, базирующееся именно на подсчёте отношения простых чисел к общему количеству.
Введём обозначения:
A1 - событие "первое число - простое, второе - любое",
A2 - событие "второе число - простое, первое - любое".
Согласно принципу включений-исключений (мы уже рассматривали его ранее - см. первую ссылку), вероятность объединения этих событий (то есть реализации хотя бы одного из них, с учётом их пересечения) вычисляется следующим образом:
Для вычисления вероятностей необходимо определиться с простыми числами. О принадлежности единицы могут возникнуть сомнения:
Таким образом:
2, 3, 5 - простые,
1, 4, 6 - не простые.
Тогда событию A1 соответствует 18 исходов: 3 допустимых значения на первом кубике, 6 любых допустимых - на втором. Аналогично, 18 исходов соответствую и событию A2.
Пересечению событий соответствует 9 исходов: 3 допустимых значения на первом кубике, и столько же на втором.
Как уже отмечалось выше, всего возможно 36 исходов.
Искомая вероятность является дополнением найденной: P = 1 - (3/4) = 1/4.
В ходе вычислений можно обратить внимание на общий знаменатель. Действительно: так как искомые вероятности пропорциональны количеству элементов в соответствующих множествах, то можно использовать принцип включений-исключений для множеств. В формулах ниже мы допустим вольность: не будем вводить новые обозначения, а на некоторое время будем подразумевать под A1 и A2 - не сами события, а множества состояний системы (из двух брошеных кубиков), которые удовлетворяют соответствующим событиям.
Вычислим количество элементов в интересующем нас множестве (дополнении): 36 - 27 = 9.
А теперь - нормируем результат по количеству элементов в универсуме: 9/36 = 1/4.
На самом деле, не имеет смысла рассматривать систему из двух кубиков. Гораздо проще воспринимать кубики - как один и тот же в двух последовательных бросках: ведь между состояниями первого и второго кубика нет никакой связи. Подобно тому, как число, выпавшее на первом кубике, не даёт нам дополнительной информации о результате броска второго, так и значение, выпавшее при первом броске кости не влияет на последующее. Вот такие переходы между пространством (два кубика в один момент времени) и временем (один кубик в два момента времени):
Пространство - это неравенство вещи другим вещам, а время - это неравенство вещи самой себе.
Итак, из 6 возможных чисел - три простых. Последнее позволяет утверждать, что, для системы из одного кубика, вероятность выпадения простого числа равна вероятности невыпадения простого числа, и равна данная вероятность - 1/2.
Таким образом, имеем 2d2 генератор, где только одно состояние (из 22=4) удовлетворяет искомому событию (P=1/4).
В общем-то, любой программист вам скажет, что двумя битами можно закодировать 4 состояния. Тот же программист припомнит булевы функции, а именно - конъюнкцию: если обозначить интересующий нас признак ("выпавшее число - не простое" [?]
Для "простое" ситуация аналогична, но в задаче про это не спрашивают
) за "1", то истинность функции "логическое И" (которая неявно фигурирует в тексте задаче) будет соответствовать искомой комбинации аргументов (значений кубиков). Конъюнкция истинна для одной из четырёх комбинаций значений аргументов. Снова 1/4, но гораздо меньшими усилиями. 


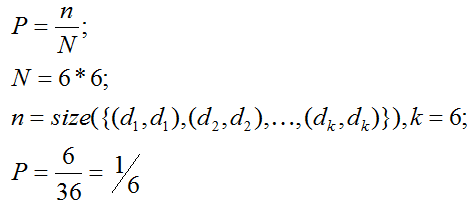
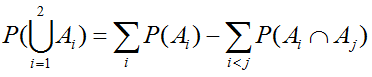
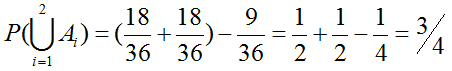
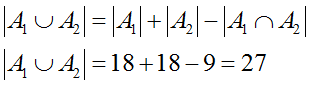

Комментарии