Вычисление площади фигуры. Часть 1

Просмотров: 1423
01 января 2017 года

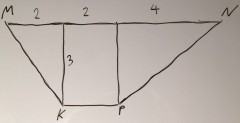
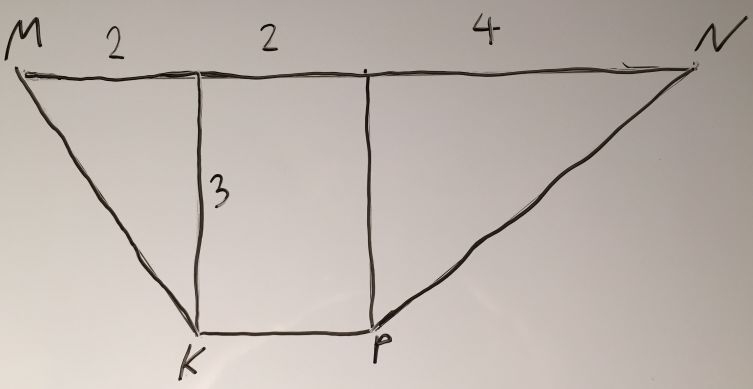
Постановка задачи

Вычислить площадь четырёхугольника, изображённого на рисунке:

Ограничения: формулы площади трапеции, треугольника и любых фигур, кроме прямоугольника - учащийся ещё не знает.
(То есть решение требует базовых знаний уровня 5-го класса.)

Общие комментарии

Во-первых, надо помнить, что площадь обладает свойством аддитивности.

Аддитивность (лат. additivus — прибавляемый) — свойство величин, состоящее в том, что значение величины, соответствующее целому объекту, равно сумме значений величин, соответствующих его частям, в некотором классе возможных разбиений объекта на части.

- Аддитивность

Иными словами: мы можем провести разбиение исходной фигуры на конечное количество фигур и вычислить сумму их площадей. Смысл такой декомпозиции - переход от вычисления площади сложной фигуры к работе с примитивами, чьи площади вычисляются относительно просто.

Площадь прямоугольника со сторонами a и b равна: S=a*b. (Предполагается, что эту формулу учащийся знает.)

Первый вариант решения

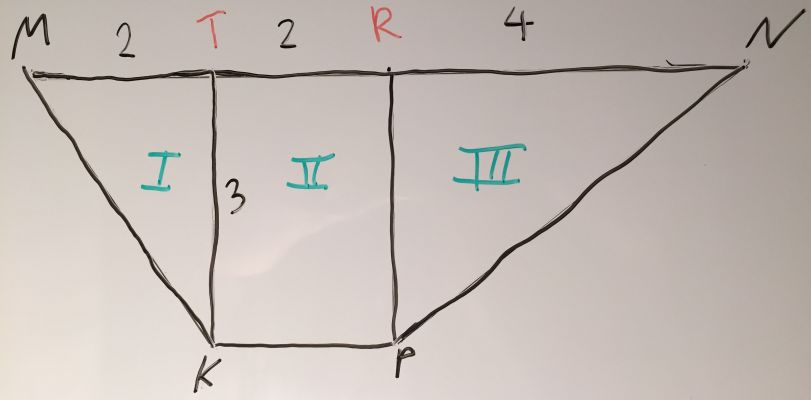
Введём две новых точки на рисунке: T и R. Теперь площадь фигуры представима суммой площадей фигур I, II и III.

S=S_MTK+S_TRPK+S_RNP

Теперь вычислим площади фигур, входящих в разбиение. Добавим ещё две точки, чтобы однозначно запутать читателя привязать рассуждения к рисунку:

S_MTK - площадь треугольника MTK, составляет половину площади прямоугольника MTKM` (согласно рисунку):

S_MTK=(1/2)*S_MTKM`=(KT*MT)/2.

Далее - прямоугольник TRPK, очевидно:

S_TRPK=KT*TR.

S_RNP вычисляется аналогично S_MTK, через площадь RNN`P. Дополнительно используем факт равенства PR и KT:

S_RNP=(1/2)*S_RNN`P=(KT*RN)/2.

Результируюущая площадь:

S = (KT*MT)/2 + KT*TR + (KT*RN)/2 =
= KT * ( MT/2 + TR + RN/2 ).

S = KT * ( MT/2 + TR + RN/2 )
S=3*(2/2+2+4/2)=3*(1+2+2)=15 ед².

Второй вариант решения

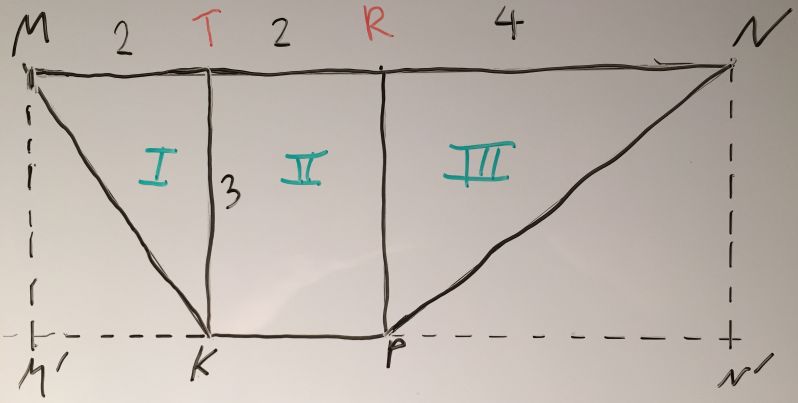
Можно "пойти другим путём" и вычесть из площади "фантомного" прямоугольника M'MNN' площади двух треугольников - M'MK и PNN':

S=S_M'MNN'-S_M'MK-S_PNN'

Не будем второй раз подробно разбирать вычисление площадей фрагментов фигуры - запишем:

S = KT*MN - (KT*MT)/2 - (KT*RN)/2 =
= KT * ( -MT/2 + MN -RN/2 ) =
представим MN как сумму отрезков
= KT * ( -MT/2 + MT + TR + RN -RN/2 ) =
упростим
= KT * ( MT/2 + TR + RN/2 ).

S = KT * ( MT/2 + TR + RN/2 )
S=3*(2/2+2+4/2)=15 ед².

Проверка по формуле площади трапеции

Формула (одна из) площади трапеции со сторонами a, b и высотой h равна: S=(a+b)*h/2. Эту формулу учащийся не знает, но воспользуемся ею здесь для демонстрации правильности решения.

S = ( KP + MT + TR + RN ) * KT/2 =
внесём множитель 1/2
= KT * [ MT/2 + ( KP + TR )/2 + RN/2 ] =
согласно рисунку, KP и TR равны
= KT * ( MT/2 + 2*TR/2 + RN/2 ) =
= KT * ( MT/2 + TR + RN/2).

S = KT * ( MT/2 + TR + RN/2 )
S=3*(2/2+2+4/2)=15 ед².

Вот и всё!

Запись опубликована в категориях:

ЕГЭ и прочие радости