Вычисление площади фигуры. Часть 2: Интеграл
Просмотров: 1946
05 января 2017 года
Постановка задачи
Общие комментарии
Ну, раз речь о площади - бери интегралы. Не будем здесь вдаваться в тонкости формулировок и определений, а просто используем на практике инструментарий, доступный учащемуся старших классов. Попутно вновь поднимем тему переходов от семантики к синтаксису и обратно.
Если данное решение для Вас излишне сложно - внизу есть ссылка на прошлую часть, где разобраны варианты решения для учащегося 5-го класса.
Решение
Определённый интеграл, позволит нам вычислить площадь фигуры, ограниченной некоторой функцией и осью абсцисс (соответственно, сверху и снизу), и прямыми, перпендикулярными оси абсцисс, и проходящими через точки, соответствующие нижнему и верхнему пределам интегрирования (соответственно слева и справа).
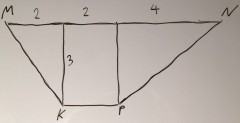
Для получения выражения, описывающего площадь данной фигуры, рассмотрим кривую, проходящую через точки M→K→P→N. Пределы интегрирования: от M до N.
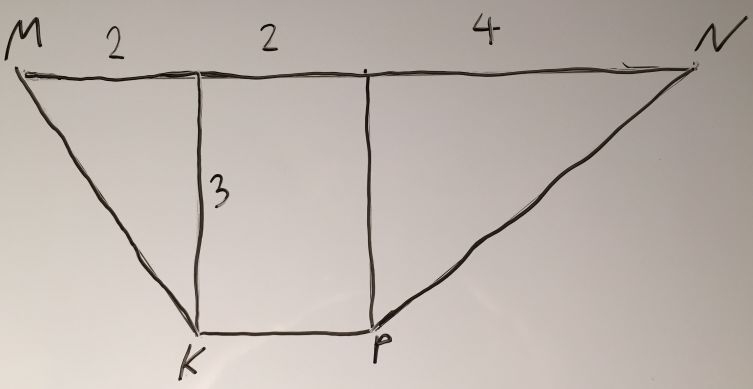
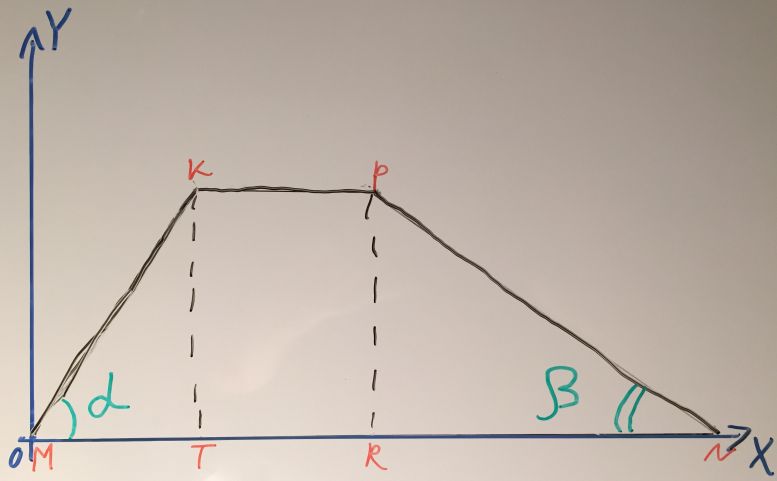
Так как фигура ограничивается кривой функции именно сверху, нам необходимо произвести некоторое преобразование, которое никак не повлияет на площадь фигуры, но позволит без проблем применить интеграл для нашей задачи. Отразим фигуру относительно оси абсцисс, как показано на рисунке ниже:
О ломаной MKPN (в плане описания для задачи) можно говорить и как о кусочно-линейной функции, и как о трёх отдельных прямых, определённых на соответствующих отрезках. В любом случае, решение разбивается на нахождение трёх интегралов. Рассмотрим вариант с интерпретацией в виде кусочно-линейной функции, так как он более громоздкий.
Функции y1(x), y2(x) и y3(x) определены ниже.
Запишем выражения для определённых интегралов:
Теперь соберём всё вместе и упростим:
Данная формула соответствует результату, полученному в первой части.
Таким образом, мы снова (см.) можем наблюдать, как выбор более абстрактного инструмента позволяет подойти к решению более формально (ни одной готовой формулы для вычисления площади конкретного примитива) и получить тот же самый ответ. Описание предметной области с использованием подходящего аппарата, позволило переложить (в некоторой степени) умственные усилия по разбиению на примитивы и подбору подходящей формулы, на формальные синтаксические преобразования. Тем не менее, конечный результат имеет ту же смысловую нагрузку, что и результат, полученный при помощи менее формальных методов.

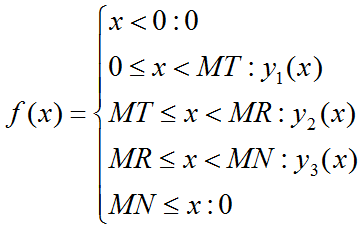
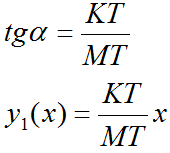
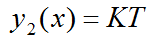
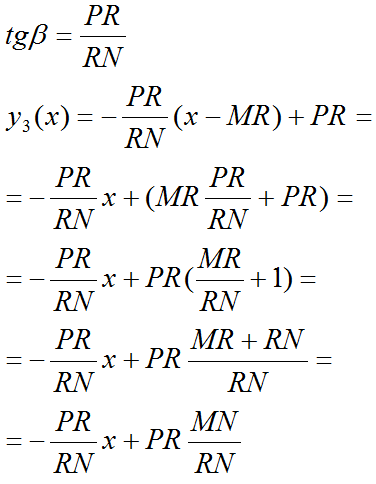
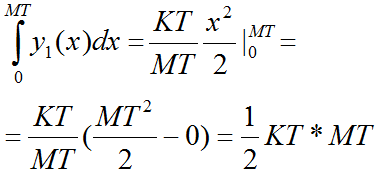
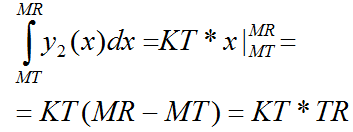
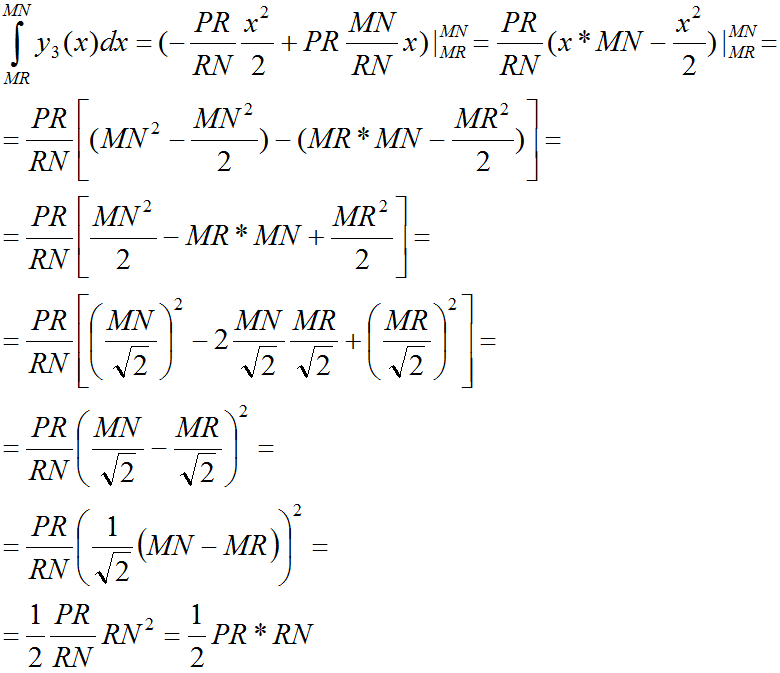
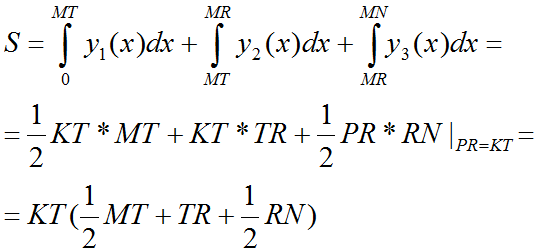
Комментарии