Вычисление площади фигуры. Часть 3: Гречка
Просмотров: 2328
14 января 2017 года
Постановка задачи
Общие комментарии
Классическое аналитическое решение (с поправкой на 5-ый класс) мы рассмотрели в первой части, изощрённое решение с привлечением интегралов - во второй. Теперь рассмотрим относительно простое (в смысле объёма вычислений и аналитики) решение, но требующее усидчивости и дающее лишь приближённый ответ. Тем не менее, сама процедура вычисления достаточно эффектна, а главное - пронизана природным смыслом происходящего, а не чёрствым синтаксисом алгебраических операций.
Метод Монте-Карло
По ссылке, приведённой в конце данной заметки, Вы сможете более детально ознакомиться с применяемым методом.
Справа Вы можете наблюдать фрагмент презентации для 10-го класса: в рамках изучения языка BASIC, рассматривается задача определения числа π методом Монте-Карло.
На практике применение данного метода у меня всегда сводилось к моделированию эксперимента на компьютере. Но для данной задачи я сделаю исключение. Во-первых, было бы странно садиться программировать, зная из всей математики только формулу площади прямоугольника и арифметчиеские операции (да кого я обманываю: судя по качеству стороннего кода и ПО - всё именно так и обстоит). Во-вторых, аналитическое описание критерия попадания в область данной фигуры нетривиально, а более "глупая" реализация через пиксельный анализ растра - медленна и громоздка.
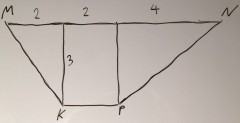
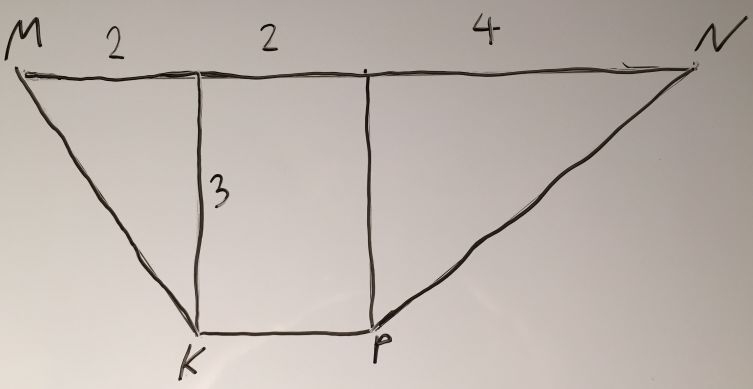
Короче говоря, я нарисовал на листочке вышеозначенную фигуру и прямоугольник, содержащий её (8×3). Получившийся рисунок я наклеил на дно коробки. Далее я взял горсть гречневой крупы, которая должна имитировать множество случайных выборов координат, и высыпал её на дно.
Практические рекомендации
Можно выделить следующие тонкости:
- Крупы должно быть адекватное количество: достаточно много, чтобы успешно применить статистические методы, но не слишком много, чтобы полностью закрыть всё дно коробки - это будет уже другой метод измерения.
- Картинка должна находиться в центре дна коробки.
- Картинка должна плотно прилегать ко дну коробки, что крупинки не цеплялись за неё, создавая артефакты распределения.
- Размеры картинки должны быть достаточно большими, чтобы вместить в себя адекватное количество крупы.
- Края фигур не должны плотно прилегать к стенкам коробки. Вокруг стенок возникают различные дополнительные эффекты: скопления тяжёлых крупинок, отскок лёгких, и т.п. - в общем равномерное распределение нарушается.
- Бросать одну крупинку за другой - слишком долго, а скидывать крупу порциями с ладони - нарушать равномерность распределения. Мой вариант: высыпать горсть в центр, после чего, движениями коробки в горизонтальной плоскости, разметать крупу по всей площади.
- Крупа должна визуально контрастировать с рисунком, быть достаточно мелкой и иметь форму, стремящуюся к шару (приближение к точке). Рис, таким образом, идеально НЕ подходит.
Результаты
На практике соблюсти все рекомендации не получилось (часть из них я сформулировал уже апостериори). Итак.
В левом треугольнике я насчитал 5 крупинок, в правом - 47, в центральной части - 177.
Таким образом, в исследуемую фигуру попало n=177, а в прямоугольник N=5+n+47=229 крупинок.
Площадь прямоугольника мы можем вычислить как SN=8*3=24.
Очевидно, что, чем больше площадь области, тем больше вероятность туда попасть. По результатам эксперимента, области, содержащие большее количество крупинок, более вероятны для попадания. Отсюда можно сделать вывод, что площадь области пропорциональна количеству крупинок, попавших в неё. Иными словами:
SN/S = N/n,
24/S = 229/177,
S = (24*177)/229,
S ≈ 18,55.
24/S = 229/177,
S = (24*177)/229,
S ≈ 18,55.
Таким образом, площадь фигуры приблизительно равна 18,55 (при аналитическом решении - 15). По мере улучшения соответствия эксперимента рекомендациям, мы будем получать более точные оценки. Дополнительно можно провести серию экспериментов и усреднить результат по реализациям.



Комментарии