Задача о лодке и течении
Просмотров: 2572
17 марта 2017 года
Теченьем лодку уносило.
Я зацепиться чудом смог.
За борт держась, собравшись с силой,
Залез в неё, на днище лёг.
Я зацепиться чудом смог.
За борт держась, собравшись с силой,
Залез в неё, на днище лёг.
- Король и Шут. «Утопленник».
Постановка задачи
Лодка шла по течению со скоростью 12,6 км/ч, а против течения - со скоростью 8,8 км/ч. Найдите скорость течения, зная, что собственная скорость лодки не изменялась.
Демагогия
Вот как: "шла по течению". Реверанс в сторону судоходного сленга?
Почему-то не уточняется: изменилась ли скорость течения реки. Откуда читателю знать, что оба эксперимента проведены в один сезон? Иными словами, допускается, что время между двумя экспериментами столь мало, что в системе не появились дополнительные эффекты, а потому правомочно описывать оба события, как события происходящие одновременно, но не влияющие друг на друга.
Терминология
Чтобы избежать дальнейших кривотолков, как это и положено, уточним терминологию. В данной задаче слишком уж много скоростей для двух предложений. В дальнейшем будем разделять следующие понятия. Собственная скорость лодки vл.с., то есть скорость, которую судно приобретает на спокойной (неподвижной) воде благодаря специальному устройству (парус, двигатель). Скорость лодки относительно берега vл.бер., то есть скорость, с которой лодка движется для стоящего на берегу наблюдателя (это движение может быть вызвано одним лишь течением реки, а может и являться суперпозицией воздействий среды и собственного движителя лодки).
Решение
На первый взгляд, всё кажется элементарным. Сначала лодка плывёт по течению, приобретая дополнительную скорость благодаря водной среде, затем - против течения, противоборствуя, и теряя скорость. И вот тут - сюрприз.
Вспомните, как в метро, часть пассажиров идёт по движущемуся эскалатору, выигрывая дополнительные секунды.
А теперь, представьте себе покупателя в торговом центре, очень спешащего на распродажу (открытие нового магазина). На пути шопоглика - эскалаторы, но, опьянённый скидками, покупатель выбирает эскалатор не с тем направлением движения полотна, и начинается состязание в упорстве. Зная тяжесть ониомании, можно предположить не только ситуацию, когда эскалатор увлекает человека вместе с собой, но и когда человек, идёт наперекор аппарату, титаническим усилием преодолевая его путы.
К чему это отступление? С математической точки зрения, модель движения человека на эскалаторе (ещё точнее - на траволаторе) и модель движения лодки по реке - идентичны. Теперь, вернёмся к лодкам.
Читаем задачу, попутно строя модель происходящего:
Лодка шла по течению со скоростью 12,6 км/ч
Ну, тут всё понятно: сложение скоростей:
vтеч+vл.с.=12,6 км/ч
Читаем дальше:
против течения - со скоростью 8,8 км/ч
Ну, а тут - вычитание скоростей. И сразу же учащийся уточняет: что из чего вычитать?
Кажущийся, чисто синтаксическим вопрос, имеет, ожидаемо, семантическую интерпретацию. Вспоминая, шопоголика на эскалаторе, мы должны определиться: поплывёт ли лодка к цели против течения, или усилий её движителя не хватит и она будет покорно уносится течением от заветной цели всё далее и далее?
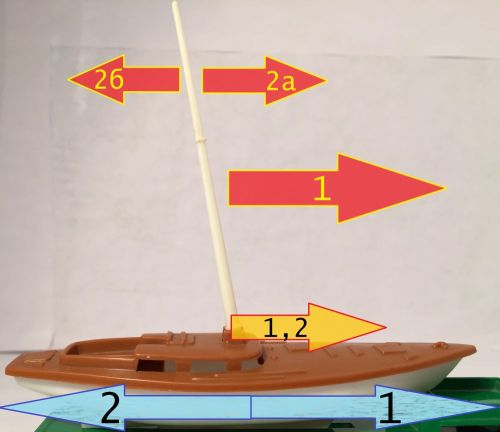
Чтобы стало совсем понятно, я набросал схемку (надеюсь, у Вас цветной монитор):
Ситуация 1. Течение реки (1, голубая стрелка) совпадает с движением лодки (1, оранжевая стрелка). Результирующее движение (1, красная стрелка) ожидаемо имеет ориентацию "вперёд".
Ситуация 2. Течение реки (2, голубая стрелка) не совпадает с движением лодки (2, оранжевая стрелка). Результирующее движение имеет ориентацию "вперёд" (2а, красная стрелка) или "назад" (2б, красная стрелка). Оба исхода не противоречат определению vл.бер., которое мы сформулировали ранее. Итоговое направление определяется соотношением скорости течения и собственной скорости лодки. Но мы не знаем этих величин!
Как это получилось?
"Что за ерунда?! Аналогичные задачки про два автомобиля решались однозначно!" Если Вы внимательно читали мою заметку про два автомобиля, то должны были усвоить тезисы (по крайней мере - я старался это показать):
- Отсутствие аппарата отрицательных чисел приводит к необходимости принятия индивидуального решения для конкретных значений скоростей (невозможно априорно синтезировать алгоритм решения без ветвлений).
- В одномерном мире, скорость - по-прежнему вектор, который характеризуется не только длиной (обычно эту величину, в подобных задачках, и называют "скоростью"), но и направлением (которое, в данном случае, должно кодироваться знаком, но - смотри пункт 1).
Поэтому подобные задачки надо формулировать с величайшей осторожностью. В случае с автомобилями, результирующая скорость вычислялась исходя из скоростей участников: учащийся просто бы не смог вычесть из меньшего большее - вместо этого он менял операнды местами, а знак "минус" (который образовывался при таких пертурбациях) интерпретировал как замену "сближения" на "удаление" и наоборот. Если Вы ничего не поняли, то прочтите заметку про автомобили и впитайте идею замены унарного минуса (знак числа) на бинарный (операция).
Здесь же автор задачи говорит просто о "скорости", подразумевая, очевидность направления результирующего движения лодки.
Корректное решение
Теперь, понимая, что в задаче говорится о модуле скорости, мы можем записать систему уравнений целиком:
Единственный способ аналитически вытащить выражение из-под знака модуля - рассмотреть два несовместных события:
- Число под знаком модуля положительно - оставляем исходное выражение.
- Число под знаком модуля отрицательно - умножаем исходное выражение на -1.
С точки зрения семантики, эти подходы и есть рассмотрение двух вариантов ответа на вопрос "что из чего вычитать?" или "куда плывёт лодка для наблюдателя на берегу?".
Рассмотрим решение двух несовместных систем:
Внимание: правильный ответ
В учебнике, ожидаемо, указан лишь один правильный ответ. Аналогичная ситуация и на сайтах с решениями задач.
У этой задачи, в виду дефицита (неполноты) предоставленной информации, два варианта правильного ответа.
Ответ из учебника соответствует шаблонной ситуации: сначала лодка летит по волнам вместе с течением (vл.бер.=1,9+10,7=12,6), затем, слегка теряя в скорости (vл.бер.=10,7-1,9=8,8), уверенно покоряет реку в обратном направлении.
Второй ответ (который привожу я) повествует о лодке, сначала ускоренной течением полноводной реки (vл.бер.=10,7+1,9=12,6), затем - тщетно пытающейся преодолеть стихию (vл.бер.=10,7-1,9=8,8).
Таким образом, в данной формулировке, задача допускает два варианта ответа:
vтеч=1,9 км/ч и vтеч=10,7 км/ч
Где все?
Большинство людей - оптимисты (ну или просто - шаблонно мыслят): в их сознании, фраза "против течения" автоматически трансформируются в картину мужественного преодоления стихии. В общем же случае, допустима ситуация, в которой борьба с течением может всего лишь позволить выиграть время, но не приблизить к цели ни на йоту.
И не надо меня уверять, что ситуация лишена смысла: данный манёвр (дрейф) можно оправдать различными ситуациями. Добавлю к этому: в задаче сказано, что скорость лодки не менялась в рамках указанных заплывов, но не сказано, что это единственно доступный скоростной режим (возможно, спустя некоторое время, собственная скорость будет увеличена и лодка покорит течение).
Что делать?
- Похвалить учащегося за умение ставить правильные вопросы.
- Показать эту заметку учителю математики.
- Надеяться, что в каком-нибудь тесте не надо будет выбирать один из двух правильных вариантов ответа.
- Отправляться запускать кораблики по ручьям - весна же.



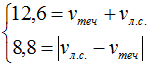
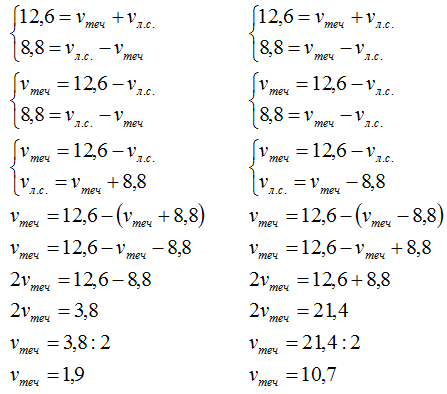

Комментарии