Способности машины и человека к случайному выбору
Просмотров: 1217
2018 год
Набатчиков А.М., Бурлак Е.А. Способности машины и человека к случайному выбору // Философия и социология техники в XXI веке. К 70-летию В.Г. Горохова / Под общей редакцией И.Ю. Алексеевой, А.А. Костиковой, А.Ф. Яковлевой. — М.: Аквилон, 2018. — С. 371–377
Мероприятие: МГУ, Международная научная конференция памяти В. Г. Горохова "Философия и социология техники в XXI веке"
Стремительное развитие науки и техники значительно увеличило роль человека в информационных и управляющих процессах [1,2]. В связи с этим всё больший интерес вызывают проблемы формализации алгоритмов принятия решения человеком-оператором [3], особенности применяемых им моделей [4] и сопутствующие человеку ограничения [5].
Отсутствие в бихевиоральной модели человека понятия «случайность» кажется логичным предположением: поведение индивида подчиняется оптимальной стратегии, определяемой набором внутренних установок и комплексом внешних факторов. Понятие случайности вводится для описания событий, логика появления которых либо неизвестна, либо слишком сложна для применения её в качестве алгоритма прогноза.
Из высказанного предположения можно сделать вывод о неспособности человека, несмотря на его свободу воли, создавать случайные события, пусть даже он мнит их таковыми. Вместе с тем, человек использует искусственные генераторы случайных чисел для огромного количества приложений, например, протоколы многофакторной аутентификации, моделирование естественных процессов [6], в том числе, имитация мышления человека [7].
Определим «качественный» генератор случайных чисел, как источник, обладающий максимальной информационной энтропией, и, что более важно, порождающий последовательность, имеющую автокорреляционную функцию, стремящуюся к дельта-функции Дирака. Таким образом, ни анализ текущего распределения значений, ни частотный анализ последовательности, не позволят повысить вероятность угадать следующее число, соответствующую 1/n (для n возможных состояний генератора).
Существующие простые арифметические генераторы псевдослучайных чисел (ГПСЧ), в силу своей детерминированности, ожидаемо, не являются достаточно качественными [8,9] : например, линейный конгруэнтный генератор может быть «взломан» по небольшому фрагменту порождаемой последовательности. В связи с этим, выглядит интересным вопрос о преимуществе человека или машины в задаче генерации качественной последовательности случайных чисел.
Несмотря на тривиальность задачи, существующие когнитивные искажения в интерпретации понятия «случайность» не позволяют человеку создавать достаточно качественную последовательность.
Экспериментальные исследования [10] выявили фактическое отстранение испытуемого от решаемой задачи в условиях отсутствия паузы перед очередным случайным выбором. В этом случае качество последовательности возрастало, ввиду изменения условий эксперимента: человек переставал осознанно выбирать случайные варианты, а становился «фильтром» окружающего его шума (в широком смысле).
Присутствие некоей мотивации подталкивало испытуемого к идентификации связи между его выборами и появлением стимула, и выработке нового алгоритма выбора.
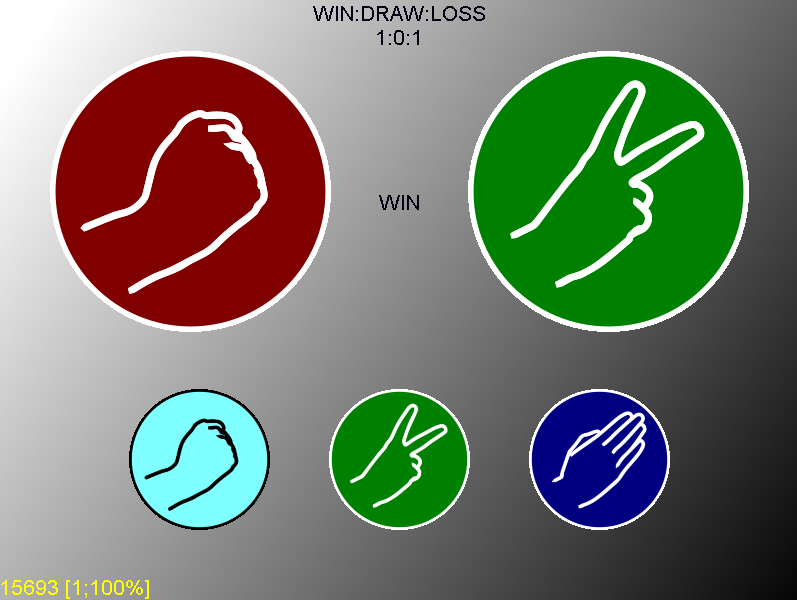
Последнее экспериментально проверено на примере игры «камень, ножницы, бумага». В рамках практического применения алгоритма прогнозирования [10], волонтёрам было предложено обыграть искусственный интеллект в компьютерной реализации данной игры (рис. 1). По заявлениям испытуемых, несмотря на ограничение времени принятия решения, они пытались подобрать выигрышный «паттерн», анализируя поведение программы. Добровольцам не сообщалось об использовании в программе алгоритмов прогнозирования.
Таким образом, можно говорить о превосходстве машины над человеком в вопросе генерации качественной случайной последовательности.
Во-первых, в [10] показано, что существуют алгоритмы, позволяющие прогнозировать последовательность чисел, порождаемую не только примитивным (в силу детерминированности) ГПСЧ, но и человеком. Возражение, что для успешного применения того или иного алгоритма прогноза необходимо априори знать тип генератора, то есть – человек ли перед нами, кажется неуместным, так как для алгоритма генерации случайных чисел, непредсказуемость – качество, сравнимое с надёжностью для алгоритма шифрования. Согласно принципу Керкгоффса, допускается, что противник может знать всё об используемой системе, кроме используемых ключей (для ГПСЧ – это начальные значения генератора). Отметим, что разработанный алгоритм не универсален и практически бессилен к иным ГПСЧ, не человеку, т.е. человек – аналог некоего арифметического генератора.
Во-вторых, такая предсказуемость порождаемой человеком последовательности, при изобилии внешней информации, могущей выступать в качестве ключей генерации, например, эмоциональное состояние, предшествующие эксперименту мысли, большое количество аудиовизуальных образов и т.п., может быть интерпретирована как примитивность используемых человеком алгоритмов.
Работа выполнена при поддержке РФФИ, проект № 15-08-06767.
Отсутствие в бихевиоральной модели человека понятия «случайность» кажется логичным предположением: поведение индивида подчиняется оптимальной стратегии, определяемой набором внутренних установок и комплексом внешних факторов. Понятие случайности вводится для описания событий, логика появления которых либо неизвестна, либо слишком сложна для применения её в качестве алгоритма прогноза.
Из высказанного предположения можно сделать вывод о неспособности человека, несмотря на его свободу воли, создавать случайные события, пусть даже он мнит их таковыми. Вместе с тем, человек использует искусственные генераторы случайных чисел для огромного количества приложений, например, протоколы многофакторной аутентификации, моделирование естественных процессов [6], в том числе, имитация мышления человека [7].
Определим «качественный» генератор случайных чисел, как источник, обладающий максимальной информационной энтропией, и, что более важно, порождающий последовательность, имеющую автокорреляционную функцию, стремящуюся к дельта-функции Дирака. Таким образом, ни анализ текущего распределения значений, ни частотный анализ последовательности, не позволят повысить вероятность угадать следующее число, соответствующую 1/n (для n возможных состояний генератора).
Существующие простые арифметические генераторы псевдослучайных чисел (ГПСЧ), в силу своей детерминированности, ожидаемо, не являются достаточно качественными [8,9] : например, линейный конгруэнтный генератор может быть «взломан» по небольшому фрагменту порождаемой последовательности. В связи с этим, выглядит интересным вопрос о преимуществе человека или машины в задаче генерации качественной последовательности случайных чисел.
Несмотря на тривиальность задачи, существующие когнитивные искажения в интерпретации понятия «случайность» не позволяют человеку создавать достаточно качественную последовательность.
Экспериментальные исследования [10] выявили фактическое отстранение испытуемого от решаемой задачи в условиях отсутствия паузы перед очередным случайным выбором. В этом случае качество последовательности возрастало, ввиду изменения условий эксперимента: человек переставал осознанно выбирать случайные варианты, а становился «фильтром» окружающего его шума (в широком смысле).
Присутствие некоей мотивации подталкивало испытуемого к идентификации связи между его выборами и появлением стимула, и выработке нового алгоритма выбора.
Последнее экспериментально проверено на примере игры «камень, ножницы, бумага». В рамках практического применения алгоритма прогнозирования [10], волонтёрам было предложено обыграть искусственный интеллект в компьютерной реализации данной игры (рис. 1). По заявлениям испытуемых, несмотря на ограничение времени принятия решения, они пытались подобрать выигрышный «паттерн», анализируя поведение программы. Добровольцам не сообщалось об использовании в программе алгоритмов прогнозирования.
Таким образом, можно говорить о превосходстве машины над человеком в вопросе генерации качественной случайной последовательности.
Во-первых, в [10] показано, что существуют алгоритмы, позволяющие прогнозировать последовательность чисел, порождаемую не только примитивным (в силу детерминированности) ГПСЧ, но и человеком. Возражение, что для успешного применения того или иного алгоритма прогноза необходимо априори знать тип генератора, то есть – человек ли перед нами, кажется неуместным, так как для алгоритма генерации случайных чисел, непредсказуемость – качество, сравнимое с надёжностью для алгоритма шифрования. Согласно принципу Керкгоффса, допускается, что противник может знать всё об используемой системе, кроме используемых ключей (для ГПСЧ – это начальные значения генератора). Отметим, что разработанный алгоритм не универсален и практически бессилен к иным ГПСЧ, не человеку, т.е. человек – аналог некоего арифметического генератора.
Во-вторых, такая предсказуемость порождаемой человеком последовательности, при изобилии внешней информации, могущей выступать в качестве ключей генерации, например, эмоциональное состояние, предшествующие эксперименту мысли, большое количество аудиовизуальных образов и т.п., может быть интерпретирована как примитивность используемых человеком алгоритмов.
Работа выполнена при поддержке РФФИ, проект № 15-08-06767.
Литература
- А.М. Набатчиков, Е.А. Бурлак. Навыки и роль человека-оператора в информационном обществе // Искусственный интеллект: философия, методология, инновации / Сборник трудов VI Всероссийской междисциплинарной конференции студентов, аспирантов и молодых учёных, г. Москва, МГТУ МИРЭА, 29-30 ноября 2012 г. // Под ред. Д.И. Дубровского и Е.А. Никтиной. Часть II (секции 4-6). – М.: МГТУ МИРЭА, 2012. – С. 81-85.
- Е.А. Бурлак, А.М. Набатчиков. Проблемы взаимодействия и распределения ролей человека и машины в динамических системах // Искусственный интеллект: философия, методология, инновации / Материалы Пятой Всероссийской конференции студентов, аспирантов и молодых учёных, г. Москва, МГТУ МИРЭА, 9-11 ноября 2011 г. Под ред. Д.И. Дубровского и Е.Д. Никитиной — М.: «Радио и Связь», 2011. – С. 244-247.
- Себряков Г.Г., Бурлак Е.А., Набатчиков А.М. Исследование стратегии выработки управляющих команд человеком-оператором при многомерном слежении // Труды Второй Международной научно-практической конференции "Человеческий фактор в сложных технических системах и средах" (Эрго-2016) (Санкт-Петербург, Россия, 6-9 июля 2016) / Под ред. А. Н. Анохина, П. И. Падерно, С. Ф. Сергеева. – СПб.: Межрегиональная эргономическая ассоциация, ФГАОУ ДПО "ПЭИПК", Северная звезда, 2016. – С. 154-157.
- Себряков Г. Г., Набатчиков А. М., Бурлак Е. А. Концептуальная модель объекта управления при формализации деятельности человека-оператора в динамическом контуре слежения // Шестая Всероссийская мультиконференция по проблемам управления (30 сентября – 5 октября 2013 г.) / Материалы мультиконференции: в 4 т. – Pостов-на-Дону: Издателъство Южного федерального университета, 2013. Т.2. – С. 95-100.
- Корсун О.Н., Бурлак Е.А., Набатчиков А.М., Столяров Г.В. Инстурментальный заход на посадку в условиях дефицита пилотажной информации // Труды Второй Международной научно-практической конференции "Человеческий фактор в сложных технических системах и средах" (Эрго-2016) (Санкт-Петербург, Россия, 6-9 июля 2016) / Под ред. А. Н. Анохина, П. И. Падерно, С. Ф. Сергеева. – СПб.: Межрегиональная эргономическая ассоциация, ФГАОУ ДПО "ПЭИПК", Северная звезда, 2016. – С. 147-154.
- Жовинский В. Н. Генерирование шумов для исследования автоматических систем. М., «Энергия», 1968.
- Тьюринг А. М. Может ли машина мыслить? // Может ли машина мыслить?: Сборник. – М.: Государственное издательство физико-математической литературы, 1960. – С. 19-58.
- Дональд Кнут. Искусство программирования, том 2. Получисленные алгоритмы = The Art of Computer Programming, vol.2. Seminumerical Algorithms. — 3-е изд. — М.: «Вильямс», 2007. — С. 832.
- Максимов М. Случайны ли «случайные» числа? // «Наука и Жизнь». — Издательство «Правда», 1986 г. №10. — с. 112
- А.М. Набатчиков, Е.А. Бурлак. Экспериментальные исследования прогнозирования случайного выбора человеком // Искусственный интеллект: философия, методология, инновации. / Сборник трудов X Всероссийской конференции студентов, аспирантов и молодых учёных. Москва, МИРЭА, 27-28 апреля 2017 г. Под общей редакцией Е.А. Никитиной. – М.: Московский технологический университет (МИРЭА), 2017. – С. 42-48.
Комментарии